Advertisements
Advertisements
प्रश्न
यदि एक समचतुर्भुज की एक भुजा 10 cm और एक विकर्ण 16 cm है, तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
समचतुर्भुज का क्षेत्रफल ज्ञात करने के लिए, हम इसे दो त्रिभुजों में विभाजित करते हैं।
चूँकि एक समचतुर्भुज की सभी भुजाएँ बराबर होती हैं, हमारे पास एक त्रिभुज होता है।
a = 10, b = 10, c = 16
`s = (a + b + c)/2`
⇒ `s = (10 + 10 + 16)/2 = 36/2 = 18`
क्षेत्रफल (Δ) = `sqrt(s(s - a)(s - b)(s - c))`
⇒ क्षेत्रफल (Δ) = `sqrt(18(18 - 10)(18 - 10)(18 - 16))`
⇒ क्षेत्रफल (Δ) = `sqrt(18 xx 8 xx 8 xx 2)`
⇒ क्षेत्रफल (Δ) = 48 cm2
चूँकि दूसरे त्रिभुज की भुजाएँ भी समान हैं, इसलिए उनके क्षेत्रफल भी बराबर होंगे।
क्षेत्रफल (समचतुर्भुज) = क्षेत्रफल (Δ) + क्षेत्रफल (Δ)
⇒ क्षेत्रफल (समचतुर्भुज) = 48 + 48 = 96 cm2
APPEARS IN
संबंधित प्रश्न
एक यातायात संकेत बोर्ड पर 'आगे स्कूल है’ लिखा है और यह भुजा ‘a‘ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
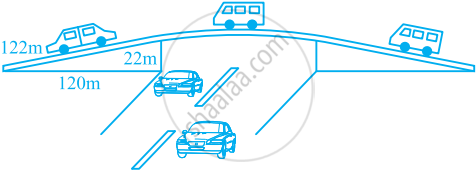
किसी फ्लाईओवर (Flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लंबाइयाँ 122 m, 22 m और 120 m हैं (देखिए आकृति)। इस विज्ञापन से प्रति वर्ष ₹ 5000 प्रति m2 की प्राप्ति होती है। एक कंपनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
भुजा a वाले एक समषड्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
एक समबाहु त्रिभुज के अभ्यंतर में स्थित किसी बिंदु से तीनों भुजाओं पर लंब डाले जाते हैं। इन लंबों की लंबाई 14 cm, 10 cm और 6 cm हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
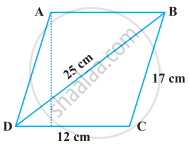
आकृति में दिए हुए समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही, शीर्ष A से भुजा DC पर शीर्षलंब की लंबाई ज्ञात कीजिए।
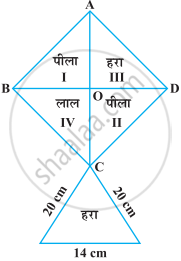
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।