SSC (Marathi Semi-English) इयत्ता १० वी - Maharashtra State Board Important Questions for Geometry Mathematics 2

A roller of diameter 0.9 m and the length 1.8 m is used to press the ground. Find the area of the ground pressed by it in 500 revolutions.
`(pi=3.14)`

Draw the circumcircle of ΔPMT in which PM = 5.6 cm, ∠P = 60°, ∠M = 70°.

The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.

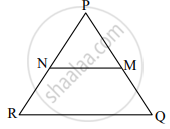
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.

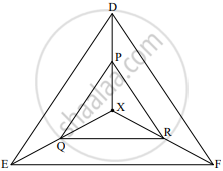
In the given figure, X is any point in the interior of the triangle. Point X is joined to the vertices of triangle. seg PQ || seg DE, seg QR || seg EF. Complete the activity and prove that seg PR || seg DF.

Proof:

In ΔXDE, PQ || DE ......(Given)

∴ `"XP"/"PD" = square/"QE"` ......(Basic proportionality theorem)…(i)

In ΔXEF, QR || EF ......(Given)

∴ `"XQ"/square = "XR"/square` ..........(`square`)....(ii)

∴ `"XP"/"PD" = square/square` ......[From (i) and (ii)]

∴ seg PR || seg DF ......(By converse of basic proportionality theorem

In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.

If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?

In fig, seg DE || sec BC, identify the correct statement.

In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x

ΔPQR ~ ΔSUV. Write pairs of congruent angles

Write the test of similarity for triangles given in figure.

In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.

In ΔAPB and ΔAQC

∠APB = [   ]°     ......(i)

∠AQC = [   ]°  ......(ii)

∠APB ≅ ∠AQC    .....[From (i) and (ii)]

∠PAB ≅ ∠QAC    .....[______]

ΔAPB ~ ΔAQC     .....[______]

From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.

In ΔPQB, PQ || side BC

`"AP"/"PB" = "AQ"/(["______"])`    ...[______]

`(x + 3)/(x - 3) = (x + 5)/(["______"])`

(x + 3) [______] = (x + 5)(x – 3)

x² + x – [______] = x² + 2x – 15

x = [______]

In ΔABC, B − D − C and BD = 7, BC = 20, then find the following ratio.

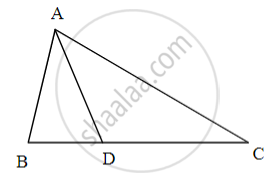
(i) `"A(ΔABD)"/"A(ΔADC)"`

(ii) `"A(ΔABD)"/"A(ΔABC)"`

(iii) `"A(ΔADC)"/"A(ΔABC)"`

In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ

In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`

Areas of two similar triangles are equal then prove that triangles are congruent

In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.

If ΔABC ∼ ΔDEF and ∠A = 48°, then ∠D = ______.

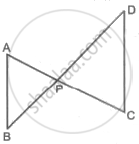
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.

Activity: In ΔABP and ΔCDP

`("AP")/("CP") = ("BP")/("DP")` ......`square`

∴ ∠APB ≅ `square` ......Vertically opposite angles

∴ `square` ∼ ΔCDP  ....... `square` test of similarity.