Advertisements
Advertisements
प्रश्न
A roller of diameter 0.9 m and the length 1.8 m is used to press the ground. Find the area of the ground pressed by it in 500 revolutions.
`(pi=3.14)`
उत्तर
Diameter = 0.9 m ∴r = 0.45 m
Height =1.8 m
Number of rotations = 500
Area of the ground pressed by the roller in one rotation = curved surface area of the roller.
= `2pi "rh"`
= 2 × 3.14 × 0.45 × 1.8
= 5.0868 m2
∴ Area of the ground pressed by the roller in 500 rotations.
= 500 × 5.0868 m2
= 2543.4 m2
∴ Area of the ground pressed by the roller is 2543.4 m2
APPEARS IN
संबंधित प्रश्न
The ratio of the areas of two triangles with the common base is 14 : 9. Height of the larger triangle is 7 cm, then find the corresponding height of the smaller triangle.
The ratio of the areas of two triangles with common base is 6:5. Height of the larger triangle of 9 cm, then find the corresponding height of the smaller triangle.
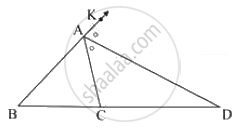
In the given figure, AD is the bisector of the exterior ∠A of ∆ABC. Seg AD intersects the side BC produced in D. Prove that :
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
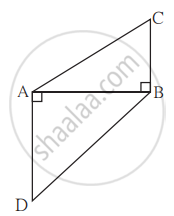
In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find `("A"(∆"ABC"))/("A"(∆"ADB"))`
In adjoining figure, PQ ⊥ BC, AD ⊥ BC then find following ratios.
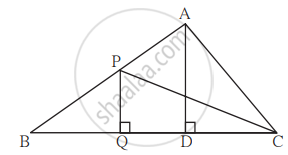
- `("A"(∆"PQB"))/("A"(∆"PBC"))`
- `("A"(∆"PBC"))/("A"(∆"ABC"))`
- `("A"(∆"ABC"))/("A"(∆"ADC"))`
- `("A"(∆"ADC"))/("A"(∆"PQC"))`
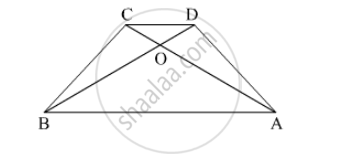
In trapezium ABCD, side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15 then Find OD.
In ∆ABC, B - D - C and BD = 7, BC = 20 then find following ratio.
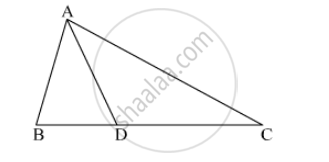
`"A(∆ ABD)"/"A(∆ ADC)"`
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?
The ratio of the areas of two triangles with the common base is 4 : 3. Height of the larger triangle is 2 cm, then find the corresponding height of the smaller triangle.
In ∆ABC, B – D – C and BD = 7, BC = 20, then find the following ratio.
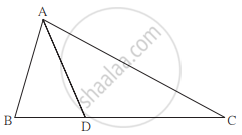
`(A(∆ABD))/(A(∆ABC))`
In ∆ABC, B – D – C and BD = 7, BC = 20 then Find following ratio.

\[\frac{A\left( ∆ ADC \right)}{A\left( ∆ ABC \right)}\]
Areas of two similar triangles are in the ratio 144: 49. Find the ratio of their corresponding sides.
In fig. BD = 8, BC = 12, B-D-C, then `"A(ΔABC)"/"A(ΔABD)"` = ?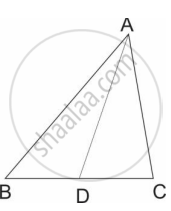
In fig., PM = 10 cm, A(ΔPQS) = 100 sq.cm, A(ΔQRS) = 110 sq.cm, then NR?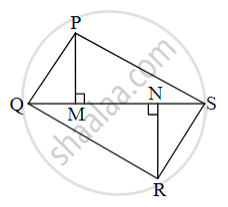
ΔPQS and ΔQRS having seg QS common base.
Areas of two triangles whose base is common are in proportion of their corresponding [______]
`("A"("PQS"))/("A"("QRS")) = (["______"])/"NR"`,
`100/110 = (["______"])/"NR"`,
NR = [ ______ ] cm
From adjoining figure, ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?

In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
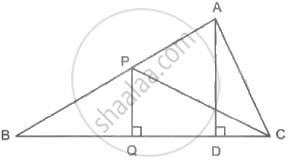
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
