Advertisements
Advertisements
प्रश्न
In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
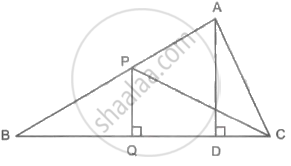
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
उत्तर
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2` × BQ × PQ
A(ΔPBC) = `1/2` × BC × PQ
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx bb(BQ) xx bb(PQ))/(1/2 xx bb(BC) xx bb(PQ))`
= `bb(BQ)/bb(BC)`
APPEARS IN
संबंधित प्रश्न
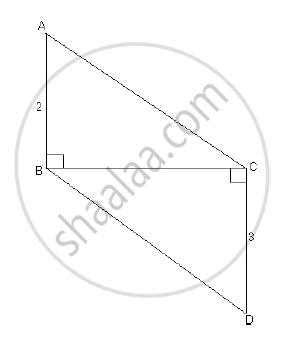
In the following figure seg AB ⊥ seg BC, seg DC ⊥ seg BC. If AB = 2 and DC = 3, find `(A(triangleABC))/(A(triangleDCB))`
The ratio of the areas of two triangles with common base is 6:5. Height of the larger triangle of 9 cm, then find the corresponding height of the smaller triangle.
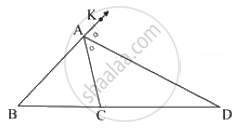
In the given figure, AD is the bisector of the exterior ∠A of ∆ABC. Seg AD intersects the side BC produced in D. Prove that :
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
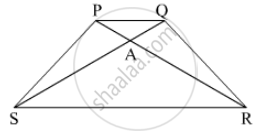
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?
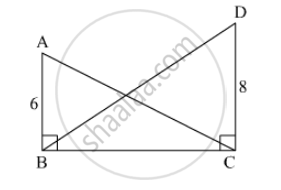
In the given figure, ∠ABC = ∠DCB = 90° AB = 6, DC = 8 then `("A(Δ ABC)")/("A(Δ DCB)")` = ?
The ratio of the areas of two triangles with the common base is 4 : 3. Height of the larger triangle is 2 cm, then find the corresponding height of the smaller triangle.
In ∆ABC, B – D – C and BD = 7, BC = 20 then Find following ratio.
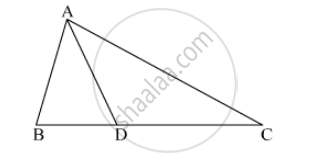
\[\frac{A\left( ∆ ADC \right)}{A\left( ∆ ABC \right)}\]
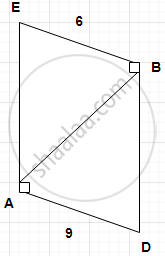
In the given, seg BE ⊥ seg AB and seg BA ⊥ seg AD.
if BE = 6 and AD = 9 find `(A(Δ ABE))/(A(Δ BAD))`.
Areas of two similar triangles are in the ratio 144: 49. Find the ratio of their corresponding sides.
In fig., TP = 10 cm, PS = 6 cm. `"A(ΔRTP)"/"A(ΔRPS)"` = ?
In fig., PM = 10 cm, A(ΔPQS) = 100 sq.cm, A(ΔQRS) = 110 sq.cm, then NR?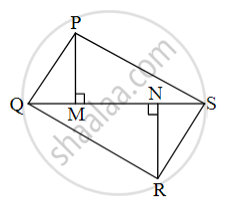
ΔPQS and ΔQRS having seg QS common base.
Areas of two triangles whose base is common are in proportion of their corresponding [______]
`("A"("PQS"))/("A"("QRS")) = (["______"])/"NR"`,
`100/110 = (["______"])/"NR"`,
NR = [ ______ ] cm
From adjoining figure, ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?

In ΔABC, B − D − C and BD = 7, BC = 20, then find the following ratio.
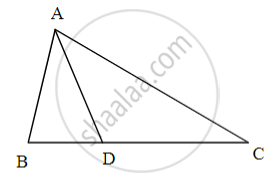
(i) `"A(ΔABD)"/"A(ΔADC)"`
(ii) `"A(ΔABD)"/"A(ΔABC)"`
(iii) `"A(ΔADC)"/"A(ΔABC)"`
If ΔABC ∼ ΔDEF, length of side AB is 9 cm and length of side DE is 12 cm, then find the ratio of their corresponding areas.
