Advertisements
Advertisements
प्रश्न
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
उत्तर १

Let ABC and PQR be two right triangles with AD ⊥ BC and PS ⊥ QR.
BC = 9, AD = 5, PS = 6 and QR = 10.
The ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
`("A"(Δ"ABC"))/("A"(Δ"PQR")) = ("AD" × "BC")/("PS" × "QR")`
∴ `("A"(Δ"ABC"))/("A"(Δ"PQR")) = (5 × 9)/(6 × 10)`
∴ `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 3/4`
Hence, Ratio of Area of △ABC : Area of △PQR = 3 : 4.
उत्तर २
Let the base, height, and area of the first triangle be b1, h1, and A1 respectively. Let the base, height and area of the second triangle be b2, h2, and A2 respectively.
b1 = 9, h1 = 5, b2 = 10 and h2 = 6.
The ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
`("A"_1)/("A"_2) = ("b"_1 × "h"_1)/("b"_2 × "h"_2)`
∴ `("A"_1)/("A"_2) = (9 × 5)/(10 × 6)`
∴ `("A"_1)/("A"_2) = 3/4`
The ratio of the areas of the triangles is 3 : 4.
संबंधित प्रश्न
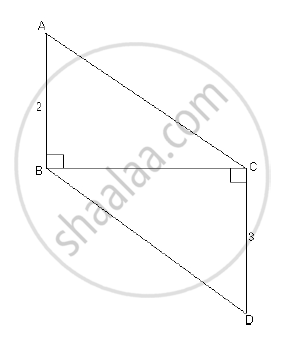
In the following figure seg AB ⊥ seg BC, seg DC ⊥ seg BC. If AB = 2 and DC = 3, find `(A(triangleABC))/(A(triangleDCB))`
The ratio of the areas of two triangles with the common base is 14 : 9. Height of the larger triangle is 7 cm, then find the corresponding height of the smaller triangle.
The ratio of the areas of two triangles with common base is 6:5. Height of the larger triangle of 9 cm, then find the corresponding height of the smaller triangle.
In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find `("A"(∆"ABC"))/("A"(∆"ADB"))`
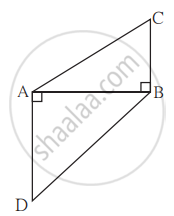
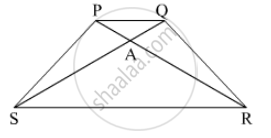
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
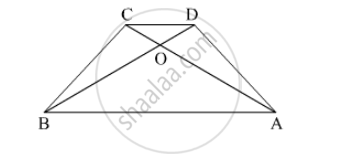
In trapezium ABCD, side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15 then Find OD.
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?
In the figure, PM = 10 cm, A(∆PQS) = 100 sq.cm, A(∆QRS) = 110 sq. cm, then find NR.
The ratio of the areas of two triangles with the common base is 4 : 3. Height of the larger triangle is 2 cm, then find the corresponding height of the smaller triangle.
In ∆ABC, B – D – C and BD = 7, BC = 20, then find the following ratio.
`(A(∆ABD))/(A(∆ABC))`
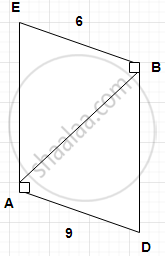
In the given, seg BE ⊥ seg AB and seg BA ⊥ seg AD.
if BE = 6 and AD = 9 find `(A(Δ ABE))/(A(Δ BAD))`.
If ΔXYZ ~ ΔPQR then `"XY"/"PQ" = "YZ"/"QR"` = ?
Areas of two similar triangles are in the ratio 144: 49. Find the ratio of their corresponding sides.
Ratio of corresponding sides of two similar triangles is 4:7, then find the ratio of their areas = ?
In fig., AB ⊥ BC and DC ⊥ BC, AB = 6, DC = 4 then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?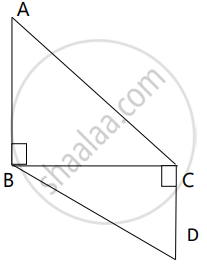
From adjoining figure, ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?

Prove that, The areas of two triangles with the same height are in proportion to their corresponding bases. To prove this theorem start as follows:
- Draw two triangles, give the names of all points, and show heights.
- Write 'Given' and 'To prove' from the figure drawn.
