Advertisements
Advertisements
प्रश्न
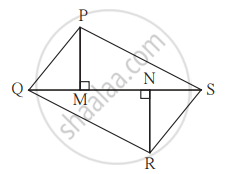
In the figure, PM = 10 cm, A(∆PQS) = 100 sq.cm, A(∆QRS) = 110 sq. cm, then find NR.
उत्तर
`{:("PM = 10 cm"), ("A(∆PQS) = 100 sq.cm"), ("A(∆QRS) = 110 sq.cm"):} }"Given"`
Now,
In ∆PQS and ∆QRS,
seg QS is common base of ∆PQS and ∆QRS.
∴ `"A(∆PQS)"/"A(∆QRS)" = "PM"/"NR"` ...(Triangles having equal base)
∴ `100/110 = 10/"NR"`
∴ `"NR" = (110 × 10)/100`
∴ NR = 11 cm
APPEARS IN
संबंधित प्रश्न
The ratio of the areas of two triangles with the common base is 14 : 9. Height of the larger triangle is 7 cm, then find the corresponding height of the smaller triangle.
In the following figure RP: PK= 3:2, then find the value of A(ΔTRP):A(ΔTPK).

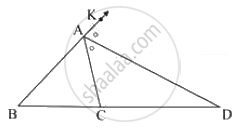
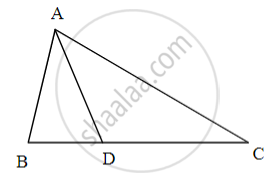
In the given figure, AD is the bisector of the exterior ∠A of ∆ABC. Seg AD intersects the side BC produced in D. Prove that :
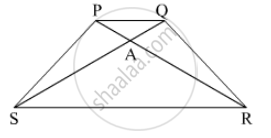
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?
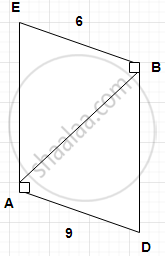
In the given, seg BE ⊥ seg AB and seg BA ⊥ seg AD.
if BE = 6 and AD = 9 find `(A(Δ ABE))/(A(Δ BAD))`.
In fig., TP = 10 cm, PS = 6 cm. `"A(ΔRTP)"/"A(ΔRPS)"` = ?
Ratio of corresponding sides of two similar triangles is 4:7, then find the ratio of their areas = ?
In fig. BD = 8, BC = 12, B-D-C, then `"A(ΔABC)"/"A(ΔABD)"` = ?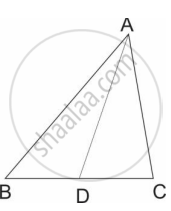
In fig., PM = 10 cm, A(ΔPQS) = 100 sq.cm, A(ΔQRS) = 110 sq.cm, then NR?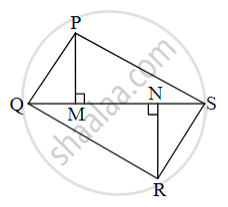
ΔPQS and ΔQRS having seg QS common base.
Areas of two triangles whose base is common are in proportion of their corresponding [______]
`("A"("PQS"))/("A"("QRS")) = (["______"])/"NR"`,
`100/110 = (["______"])/"NR"`,
NR = [ ______ ] cm
In fig., AB ⊥ BC and DC ⊥ BC, AB = 6, DC = 4 then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?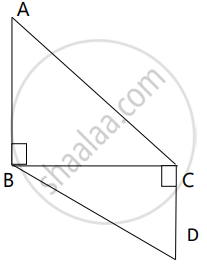
From adjoining figure, ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?

In ΔABC, B − D − C and BD = 7, BC = 20, then find the following ratio.
(i) `"A(ΔABD)"/"A(ΔADC)"`
(ii) `"A(ΔABD)"/"A(ΔABC)"`
(iii) `"A(ΔADC)"/"A(ΔABC)"`
Prove that, The areas of two triangles with the same height are in proportion to their corresponding bases. To prove this theorem start as follows:
- Draw two triangles, give the names of all points, and show heights.
- Write 'Given' and 'To prove' from the figure drawn.
If ΔABC ∼ ΔDEF, length of side AB is 9 cm and length of side DE is 12 cm, then find the ratio of their corresponding areas.
In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
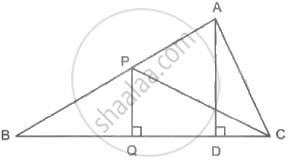
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
