Advertisements
Advertisements
Question
(2, 14) से गुजरने वाली दो रेखाओं के समीकरण दीजिए। ऐसी और कितनी पंक्तियाँ हैं, और क्यों?
Solution
यह देखा जा सकता है कि बिंदु (2, 14) समीकरण 7x − y = 0 और x − y + 12 = 0 को संतुष्ट करता है।
इसलिए, 7x − y = 0 और x − y + 12 = 0 बिंदु (2, 14) से गुजरने वाली दो रेखाएं हैं।
जैसा कि ज्ञात है कि एक बिंदु से अनंत संख्या में रेखाएं गुजर सकती हैं, इसलिए दिए गए बिंदु से गुजरने वाली इस प्रकार की अनंत रेखाएं हैं।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित रैखिक समीकरणों का दो चरों में आलेख खींचिए:- 3 = 2x + y
नीचे दिए गए विकल्पों में से उस समीकरण को चुनिए जिसके आलेख दिए गए आंकड़ों में दिए गए हैं।
पहले आंकड़े के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

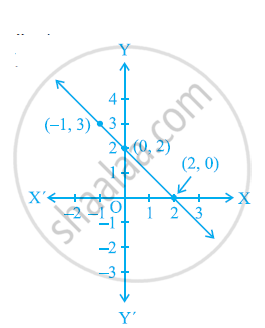
दूसरे आंकड़े के लिए
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
एक अचर बल लगाने पर एक पिंड द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है। इस कथन को दो चरों वाले एक समीकरण के रूप में व्यक्त कीजिए और अचर बल 5 मात्रक लेकर इसका आलेख खींचिए। यदि पिंड द्वारा तय की गई दूरी
(i) 2 मात्रक (ii) 0 मात्रक
हो, तो आलेख से किया हुआ कार्य ज्ञात कीजिए।
एक विद्यालय की कक्षा IX की छात्राएं यामिनी और फातिमा ने मिलकर भूकंप पीडि़त व्यक्तियों की सहायता के लिए प्रधानमंत्री राहत कोष में 100 रु अंशदान दिया। एक रैखिक समीकरण लिखिए जो इन आंकड़ों को संतुष्ट करती हो। (आप उनका अंशदान x रु और y रु मान सकते हैं)। इस समीकरण का आलेख खींचिए।
अमरीका और कनाडा जैसे देशों में तापमान फारेनहाइट में मापा जाता है, जबकि भारत जैसे देशों में तापमान सेल्सियस में मापा जाता है। यहाँ फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण दिया गया है:
`F=(9/5)C+32`
-
सेल्सियस को x-अक्ष और फारेनहाइट को y-अक्ष मानकर ऊपर दिए गए रैखिक समीकरण का आलेख खींचिए।
-
यदि तापमान 30°C है, तो फारेनहाइट में तापमान क्या होगा?
-
यदि तापमान 95°F है, तो सेल्सियस में तापमान क्या होगा?
-
यदि तापमान 0°C है, तो फारेनहाइट में तापमान क्या होगा? और यदि तापमान 0°F है, तो
सेल्सियस में तापमान क्या होगा? -
क्या ऐसा भी कोई तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकत: समान है? यदि हाँ, तो उसे ज्ञात कीजिए।
दो चरों वाली रैखिक समीकरण 2x + 0y + 9 = 0 के किसी भी हल का रूप होता है
समीकरण ax + by + c = 0 के धनात्मक हल सदैव निम्नलिखित में स्थित होते हैं
दो चरों वाली रैखिक समीकरण के आलेख का एक सरल रेखा होना आवश्यक नहीं है।
वह रैखिक समीकरण लिखिए, जिसके आलेख के प्रत्येक बिंदु की कोटि उसकी भुज की तीन गुनी है।
दर्शाइए कि बिंदु A(1, 2), B(– 1, – 16) और C(0, – 7) रैखिक समीकरण y = 9x – 7 के आलेख पर स्थित हैं।
