Advertisements
Advertisements
Question
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखंड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाईयाँ क्रमश: 8 cm और 6 cm हैं (देखिए आकृति)। भुजाएँ AB और AC ज्ञात कीजिए।
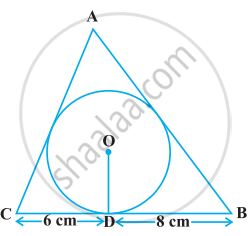
Solution
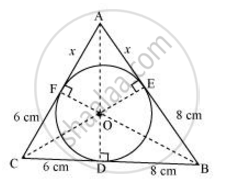
मान लीजिए दिया गया वृत्त त्रिभुज की भुजाओं AB और AC को क्रमशः बिंदु E और F पर स्पर्श करता है और रेखाखंड AF की लंबाई x है।
ΔABC में,
CF = CD = 6cm ....(बिंदु C से वृत्त पर स्पर्श रेखाएं)
BE = BD = 8cm ....(बिंदु B से वृत्त पर स्पर्श रेखाएं)
AE = AF = x ....(बिंदु A से वृत्त पर स्पर्श रेखाएँ)
AB = AE + EB = x + 8
BC = BD + DC = 8 + 6 = 14
CA = CF + FA = 6 + x
2s = AB + BC + CA
= x + 8 + 14 + 6 + x
= 28 + 2x
S = 14 + x
`"त्रिभुज का क्षेत्रफल" ABC = sqrt(s(s-1)(s-b)(s-c))`
`=sqrt({14+x}{(14+x)-14}{(14+x)-(6+x)}{(14+x)-(8+x)})`
`=sqrt((14+x)(x)(8)(6))`
`=4sqrt(3(14x+x^2))`
`"त्रिभुज OBC का क्षेत्रफल" = 1/2xxODxxBC `
`= 1/2xx4xx14 `
= 28
त्रिभुज OCA का क्षेत्रफल = `1/2xxOFxxAC `
`= 1/2xx4xx(6+x)`
`= 12+2x`
`"त्रिभुज" OAB "का क्षेत्रफल" = 1/2xxOExxAB`
` = 1/2xx4xx(8+x) `
`= 16+2x`
ABC का क्षेत्रफल = OBC का क्षेत्रफल + OCA का क्षेत्रफल + OAB का क्षेत्रफल
`4sqrt(3(14x+x^2)) = 28+12+2x+16+2x`
`4sqrt(3(14x+x^2)) = 56+4x`
`=> (3(14x+x^2)) = 14+x`
`=>3(14x+x^2) = (14+x)^2`
`=>42x+3x^2=196+x^2+28x`
`=>2x^2+14x-196 = 0`
`=>x^2+7x-98 = 0`
`=>x^2+14x-7x-98= 0`
`=>x(x+14)-7(x+14) = 0`
=>(x + 14) (x − 7) = 0
या तो x + 14 = 0 या x − 7 = 0
इसलिए, x = −14 और 7
हालांकि, x = −14 संभव नहीं है क्योंकि भुजाओं की लंबाई ऋणात्मक होगी।
इसलिए, x = 7
अत: AB = x + 8 = 7 + 8 = 15 सेमी
BC = 8 + 6 = 14 सेमी
CA = 6 + x = 6 + 7 = 13 सेमी
APPEARS IN
RELATED QUESTIONS
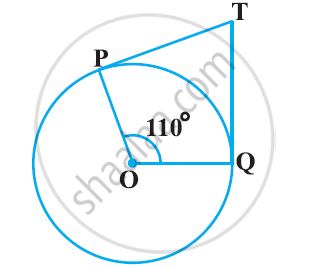
आकृति में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 1100, तो ∠PTQ बराबर है ______.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 cm की दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त स्पर्श करती हो।
सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने साम्ने की भुजाएँ केन्द्र पर संपूरक कोण अंतरित करती हैं।
यदि केंद्र O वाले एक वृत्त के एक बाहरी बिंदु B से दो स्पर्श रेखाएँ BC और BD इस प्रकार खींची जाएँ कि ∠DBC = 120° है, तो सिद्ध कीजिए कि BC + BD = BO है, अर्थात् BO = 2BC है।
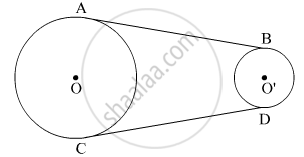
आकृति में, AB और CD असमान त्रिज्याओं वाले दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ हैं। सिद्ध कीजिए कि AB = CD हैं।
एक बाहरी बिंदु P से केंद्र O वाले वृत्त की दो स्पर्श रेखाएँ PA और PB खींची जाती हैं। वृत्त के एक बिंदु E पर एक स्पर्श रेखा खींची जाती है, जो PA और PB को क्रमश : D और E पर प्रतिच्छेद करती है। यदि PA = 10 cm है, तो त्रिभुज PCD का परिमाप ज्ञात कीजिए।
केंद्र O और त्रिज्या 5 cm वाले एक वृत्त के केंद्र से 13 cm की दूरी पर एक बिंदु A है। AP और AQ क्रमश: बिंदुओं P और Q पर वृत्त की स्पर्श रेखाएँ हैं। यदि लघु चाप PQ पर स्थित एक बिंदु R पर एक स्पर्श रेखा BC ऐसी खींची जाए, जो AP को B और AQ को C पर प्रतिच्छेद करे, तो ΔABC का परिमाप ज्ञात कीजिए।
