Advertisements
Advertisements
Question
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
Solution
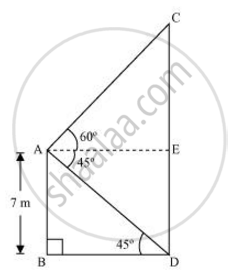
मान लीजिए AB एक भवन है और CD एक केबल टावर है।
ΔABD में,
`"AB"/"BD"` = tan 45°
`7/"BD"` = 1
BD = 7 m
ΔACE में,
AE = BD = 7 m
`"CE"/"AE"` = tan 60°
`"CE"/7 = sqrt3`
`"CE" = 7sqrt3 "m"`
CD = CE + ED
= `(7sqrt3 + 7)"m"`
= `7(sqrt3 + 1)"m"`
इसलिए, केबल टावर की ऊँचाई `7(sqrt3+1)m` है।
APPEARS IN
RELATED QUESTIONS
सर्कस का एक कलाकार एक 20m लंबी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खंभे की ऊँचाई ज्ञात कीजिए।

भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
1.5 म लंबा एक लड़का 30 म ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है जब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए की वह भवन की ओर कितनी दूरी तक चलकर गया है।
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
किसी बिंदु से एक मीनार की चोटी का उन्नयन कोण 30° है। यदि प्रेक्षक दीवार की ओर 20 मीटर चलता है, तो उन्नयन कोण में 15° की वृद्धि हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए।
एक ऊर्ध्वाधर मीनार एक क्षैतिज समतल पर खड़ी है तथा उस पर h ऊँचाई का एक ऊर्ध्वाधर ध्वज-दंड लगा हुआ है। समतल के किसी बिंदु से ध्वज-दंड के निचले और ऊपरी सिरों के उन्नयन कोण क्रमश : α और β हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `((h tan alpha)/(tan beta - tan alpha))` है।
किसी मकान की निचली खिड़की भूमि से 2 m की ऊँचाई पर है तथा उसकी ऊपरी खिड़की निचली खिड़की से ऊर्ध्वाधरत : 4 m ऊपर है। किसी क्षण इन खिड़कियों से एक गुब्बारे के उन्नयन कोण क्रमश : 60° और 30° प्रेक्षित किए गए। भूमि के ऊपर गुब्बारे की ऊँचाई ज्ञात कीजिए।
