Advertisements
Advertisements
प्रश्न
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
उत्तर
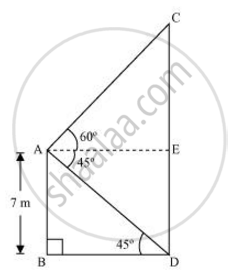
मान लीजिए AB एक भवन है और CD एक केबल टावर है।
ΔABD में,
`"AB"/"BD"` = tan 45°
`7/"BD"` = 1
BD = 7 m
ΔACE में,
AE = BD = 7 m
`"CE"/"AE"` = tan 60°
`"CE"/7 = sqrt3`
`"CE" = 7sqrt3 "m"`
CD = CE + ED
= `(7sqrt3 + 7)"m"`
= `7(sqrt3 + 1)"m"`
इसलिए, केबल टावर की ऊँचाई `7(sqrt3+1)m` है।
APPEARS IN
संबंधित प्रश्न
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है की पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 मीटर है। पेड़ की उँचाई ज्ञात कीजिए।
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
1.5 म लंबा एक लड़का 30 म ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है जब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए की वह भवन की ओर कितनी दूरी तक चलकर गया है।
भूमि के एक बिंदु से एक 20 मीटर ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमश: 45° और 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
6 m ऊँचे एक खंभे की छाया भूमि पर `2sqrt3` m लंबी है। तब, उस समय सूर्य का उन्नयन कोण ______ है।
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
यदि एक मीनार की ऊँचाई तथा उसके आधार से प्रेक्षण बिंदु की दूरी दोनों ही 10% बढ़ जाते हैं, तो चोटी का उन्नयन कोण वही रहता है।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
