Advertisements
Advertisements
प्रश्न
यदि एक झील की सतह से 3 मीटर ऊपर एक प्लेटफार्म पर खड़ा एक व्यक्ति किसी बादल और झील में उसके परावर्तन को देखता है, तो उस बादल का उन्नयन कोण उसके परावर्तन के अवनमन कोण के बराबर होता है।
विकल्प
सत्य
असत्य
उत्तर
यह कथन असत्य है।
स्पष्टीकरण:
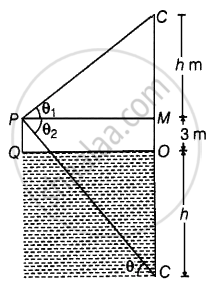
आकृति से, हम देखते हैं कि, झील की सतह से 3 मीटर ऊपर, बिंदु P पर एक मंच पर खड़ा एक व्यक्ति बिंदु C पर एक बादल देखता है।
माना कि मंच की सतह से बादल की ऊंचाई h है और बादल का उन्नयन कोण θ1 है।
अब उसी बिंदु P पर एक व्यक्ति झील में बादल का प्रतिबिंब देखता है, इस समय झील में बादल के प्रतिबिंब की ऊंचाई (h + 3) है क्योंकि झील में मंच की ऊंचाई भी बादल के प्रतिबिंब में जोड़ी जाती है।
इसलिए, झील में अवनमन का कोण झील की सतह के ऊपर बादल के उन्नयन कोण से भिन्न होता है।
ΔMPC में,
tan θ1 = `"CM"/"PM" = "h"/"PM"`
⇒ `(tan θ_1)/"h" = 1/"PM"` ...(i)
ΔCPM में,
tan θ2 = `"CM"/"PM"`
= `("OC" + "OM")/"PM"`
= `("h" + 3)/"PM"`
⇒ `(tan θ_2)/("h" + 3) = 1/"PM"` ...(ii)
समीकरण (i) और (ii) से,
`(tan θ_1)/"h" = (tan θ_2)/("h" + 3)`
⇒ tan θ2 = `(("h" + 3)/"h") tan θ_1`
अतः, θ1 ≠ θ2
APPEARS IN
संबंधित प्रश्न
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 मीटर की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध से दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर की डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
एक पेडस्टल के शिखर पर एक 1.6 मीटर ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद - बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन को ऊंचाई ज्ञात कीजिए।
एक 1.2 मीटर लंबी लड़की जमीन से 88.2 मीटर की ऊंचाई पर एक क्षैतिज रेखा में हवा के साथ चलते हुए एक गुब्बारे को देखती है। किसी भी क्षण लड़की की आँखों से गुब्बारे का उन्नयन कोण 60° होता है। कुछ समय बाद, उन्नयन कोण घटकर 30° हो जाता है। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए की मीनार की ऊँचाई 6 m है।
1.5 मीटर ऊँचाई वाला एक प्रेक्षक 22 मीटर ऊँची एक मीनार से 20.5 मीटर की दूरी पर खड़ा है। प्रेक्षक की आँख से मीनार की चोटी का उन्नयन कोण निर्धारित कीजिए।
किसी मीनार के आधार से s और t की दूरियों पर स्थित दो बिंदुओं से मीनार की चोटी के उन्नयन कोण परस्पर पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(st)` है।
30 m ऊँची एक मीनार की चोटी का उसी समतल भूमि पर खड़ी मीनार के आधार से उन्नयन कोण 60° है तथा दूसरी मीनार की चोटी का पहली मीनार के आधार से उन्नयन कोण 30° है। दोनों मीनारों के बीच की दूरी ज्ञात कीजिए तथा दूसरी मीनार की ऊँचाई भी ज्ञात कीजिए।
किसी ऊर्ध्वाधर मीनार की चोटी का भूमि पर स्थित किसी बिंदु से उन्नयन कोण 60° है। पहले बिंदु से 10 m उर्ध्वाधरत: ऊपर एक अन्य बिंदु पर उसका उन्नयन कोण 45° है। मीनार की उँचाई ज्ञात कीजिए।
