Advertisements
Advertisements
Question
A body at rest is thrown downward from the top of the tower. Draw a distance – time graph of its free fall under gravity during the first 3 seconds. Show your table of values starting t = 0 with an interval of 1 second, (g = 10 ms−2).
Solution
Initial velocity = M = 0
Acceleration = a = +g = 10 ms−2
when t = Is, then distance travelled (S), is given by
S1 = ut + `1/2` at2
S1 = `0(1)+1/2(10)(1)^2`
S1 = 5m
When t = 2s then S2 = ut + `1/2` at2
S2 = `(0)(2)+1/2(10)(2)^2`
S2 = 5(4) = 20 m
When t = 3s, then S3 = ut + `1/2` at2
S3 = `(0)(3)+1/2(10)(3)^2`
S = 5 (9) = 45 m
| Time | 1s | 2s | 3s |
| Distance covered | 5 m | 20 m | 45 m |

APPEARS IN
RELATED QUESTIONS
What can you say about the motion of a body if its speed-time graph is a straight line parallel to the time axis ?
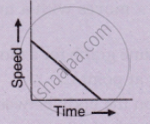
What type of motion is represented by the following graph ?
A car of mass 1000 kg is moving with a velocity of 10 m s−1. If the velocity-time graph for this car is a horizontal line parallel to the time axis, then the velocity of car at the end of 25 s will be :
A ball is thrown up vertically and returns back to thrower in 6 s. Assuming there is no air friction, plot a graph between velocity and time. From the graph calculate
- deceleration
- acceleration
- total distance covered by ball
- average velocity.
From the velocity – time graph given below, calculate Distance covered in the region ABCE.

Interpret the following graph:
Draw velocity-time graph to show:
Deceleration
Write a sentence to explain the shape of graph.
What does the slope of velocity-time graph represent?
The area under velocity – time graph represents the ______
Slope of the velocity-time graph gives ______.
