Advertisements
Advertisements
Question
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
Solution
The diameter of the base = 40 cm
∴ Radius (r) = `40/2 cm` = 20 cm = `20/100 m` = 0.2 m
Height (h) = 1 m
∴ Slant height(l) = `sqrt(r^2 + h^2)`
= `sqrt((0.2)^2 + (1)^2) m`
= `sqrt(0.04 + 1) m`
= `sqrt(1.04) m`
= 1.02 ...`sqrt1.04` = 1.02 (given)
Now, curved surface area = πrl
∴ The curved surface area of a cone
= 3.14 × 0.2 × 1.02 m2
= `314/100 xx 2/10 xx 102/100 m^2`
⇒ Curved surface area of 50 cones
= `50 xx [314/100 xx 2/10 xx 102/100] m^2`
= `(314 xx 102)/(10 xx 100) m^2`
Cost of painting 1 m2 area = ₹ 12
∴ Total cost of painting `[(314 xx 102)/1000] m^2` area
= ₹ `((12 xx 314 xx 102)/1000)`
= ₹ `384336/1000`
= ₹ 384.336
= ₹ 384.34 (approx.)
Thus, the required cost of painting is ₹ 384.34 (approx.).
APPEARS IN
RELATED QUESTIONS
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the radius of the base and total surface area of the cone.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
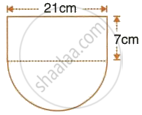
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
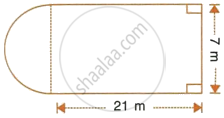
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: height of the tent.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
