Question

A car is speeding up a horizontal road with acceleration a. Consider the following situations in the car: (i) A ball suspended from the ceiling by a string is maintaining a constant angle with the vertical. Find this angle. (ii) A block is kept on a smooth incline and does not slip on the incline. Find the angle of the incline with the horizontal.

Answer 1

Let the pendulum (formed by the ball and the string) make angle θ with the vertical.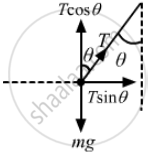

From the free-body diagram,
Tcosθ − mg = 0
Tcosθ = mg
\[\Rightarrow T = \frac{mg}{\cos \theta} . . . \left( i \right)\]
And, ma − T sin θ = 0
⇒ ma = T sin θ
\[\Rightarrow T = \frac{ma}{\sin \theta} . . . . \left( ii \right)\]
\[ \Rightarrow \tan \theta = \frac{a}{g}\]
\[ \Rightarrow \theta = \tan^{- 1} \frac{a}{g}\]
So, the angle formed by the ball with the vertical is \[\tan^{- 1} \left( \frac{a}{g} \right)\]
(ii) Let the angle of the incline be θ.
From the diagram,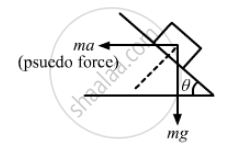

⇒ ma cos θ = mg sin θ

\[\frac{\sin \theta}{\cos \theta} = \frac{a}{g}\]

\[\tan \theta = \frac{a}{g}\theta = \tan^{- 1} \left( \frac{a}{g} \right)\]
So, the angle of incline is \[\tan^{- 1} \left( \frac{a}{g} \right)\]