Advertisements
Advertisements
Question
A charge Q is distributed uniformly over a metallic sphere of radius R. Obtain the expressions for the electric field (E) and electric potential (V) at a point 0 < x < R.
Show on a plot the variation of E and V with x for 0 < x < 2R.
Solution
Suppose, we have to calculate the electric field at the point P at a distance x (x < R) from its centre. Draw the Gaussian surface through point P to enclose the charged spherical shell. The Gaussian surface is a spherical shell of radius x and centre O.

Let `vecE` be the electric field at point P. Then, the electric flux through area element `vec(ds)`
`dø = vecE.vec(ds) `
Since `vec(dS)` is also along the normal to the surface, \[d\phi = Eds\]
∴ Total electric flux through the Gaussian surface,
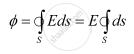
Now,
\[\oint dS = 4 \pi x^2 \]
\[ \therefore \phi = E \times 4 \pi x^2 . . . . . (i)\]
and according to Gauss's theorem,
So,
As charge inside a metallic sphere is 0
\[\Rightarrow\]E = 0
i.e. E = 0 (x < R)
We know that,
\[E = - \frac{dV}{dx}\]
\[\Rightarrow dV = - Edx\]
\[ \Rightarrow V = - \int_0^R E d x\]
\[ \Rightarrow V = - \int_0^R \frac{Q}{4\pi \epsilon_0 x^2} d x\]
\[ \Rightarrow V = \frac{Q}{4\pi \epsilon_0 R}\]
At every point within the sphere potential is same as that on surface.
Plot of variation of E with x for 0 < x < 2R

Plot of variation of V with x for 0 < x < 2R

APPEARS IN
RELATED QUESTIONS
Three concentric metallic shells A, B and C or radii a, b and c (a < b < c) have surface charge densities + σ, −σ and + σ, respectively as shown in the figure
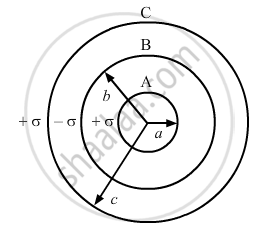
If shells A and C are at the same potential, then obtain the relation between the radii a, b and c.
In an electric circuit containing a battery, the charge (assumed positive) inside the battery ____________ .
Sunita and her friends visited the exhibition. The policeman asked them to pass through a metal detector. Sunita's friends were initially scared of it. Sunita, however, explained to them the purpose and working of the metal detector.
Answer the following questions :
(a) On what principle does a metal detector work?
(b) Why does the detector emit a sound when a person carrying any metallic object walks through it?
(c) State any two qualities which Sunita displayed while explaining the purpose of walking through the detector.
A constant voltage is applied between the two ends of a uniform metallic wire. Some heat is developed in it. The heat developed is doubled if ______.
If the resistivity of an alloy is P and that of constitute metal is P1 then
A steady current of 1 A is flowing through the conductor. The number of electrons flowing through the cross-section of the conductor in 1 second is ______
For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this?
An electric current (I) flowing through a metallic wire is gradually increased. The graph of heating power (P) developed in it versus the current (I) is ______.
Current I flowing through a metallic wire is gradually increased. Show graphically how heating power (P) developed in it varies with the current (I).
