Advertisements
Advertisements
Question
A coil having inductance 2.0 H and resistance 20 Ω is connected to a battery of emf 4.0 V. Find (a) the current at the instant 0.20 s after the connection is made and (b) the magnetic field energy at this instant.
Solution
Given:-
Self-inductance of the coil, L = 2.0 H
Resistance in the coil, R = 20 Ω
Emf of the battery, e = 4.0 V
The steady-state current is given by
\[i_0 = \frac{e}{R} = \frac{4}{20}\]
The time-constant is given by
\[\tau = \frac{L}{R} = \frac{2}{20} = 0 . 1\]
(a) Current at an instant 0.20 s after the connection is made:-
i = i0(1 − e−t/τ)
\[=\frac{4}{20}(1 − e^{−0.2/0.1})\]
\[=\frac{1}{5}(1-e^{-2})\]
= 0.17 A
(b) Magnetic field energy at the given instant:-
\[\frac{1}{2}L i^2=\frac{1}{2}\times 2(0.17)^2\]
= 0.0289 = 0.03 J
APPEARS IN
RELATED QUESTIONS
In a given coil of self-inductance of 5 mH, current changes from 4 A to 1 A in 30 ms. Calculate the emf induced in the coil.
A toroidal solenoid with air core has an average radius of 15 cm, area of cross-section 12 cm2 and has 1200 turns. Calculate the self-inductance of the toroid. Assume the field to be uniform across the cross-section of the toroid.
The currents flowing in the two coils of self-inductance L1 = 16 mH and L2 = 12 mH are increasing at the same rate. If the power supplied to the two coil is equal, find the ratio of induced voltages ?
The currents flowing in the two coils of self-inductance L1 = 16 mH and L2 = 12 mH are increasing at the same rate. If the power supplied to the two coil is equal, find the ratio of the energies stored in the two coils at a given instant ?
Define self-inductance of a coil. Show that magnetic energy required to build up the current I in a coil of self inductance L is given by `1/2 LI^2`
A plot of magnetic flux (Φ) versus current (I) is shown in the figure for two inductors A and Β. Which of the two has larger value of self inductance?

A magnetic flux of 8 × 10−4 weber is linked with each turn of a 200-turn coil when there is an electric current of 4 A in it. Calculate the self-inductance of the coil.
An inductor-coil carries a steady-state current of 2.0 A when connected across an ideal battery of emf 4.0 V. If its inductance is 1.0 H, find the time constant of the circuit.
Choose the correct option
A current through a coil of self-inductance 10 mH increases from 0 to 1 A in 0.1 s. What is the induced emf in the coil?
Explain why the inductance of two coils connected in parallel is less than the inductance of either coil.
A coil of self-inductance 3 H carries a steady current of 2 A. What is the energy stored in the magnetic field of the coil?
When the number of turns in a coil is tripled without any change in the length of the coil, its self-inductance ______
The coefficient of self-inductance of a solenoid is 0.20 mH. If a core of soft iron of relative permeability 900 is inserted, then the coefficient of self-inductance will become nearly ______
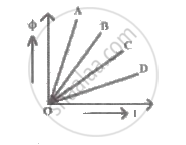
A graph of magnetic flux `(phi)` versus current (I) is shown for four inductors A, B, C and D. Larger value of self-inductance is for inductor ____________.
Two coils of self inductances 2 mH and 8 mH are placed so close together that the effective flux in one coil is completely linked with the other. The mutual inductance between these coils is ______.
An air-cored solenoid with length 30 cm, area of cross-section 25 cm2 and number of turns 800, carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10-3s. Ignoring the variation in magnetic field near the ends of the solenoid, the average back emf induced across the ends of the open switch in the circuit would be ______.
Calculate the self-inductance of a coil using the following data obtained when an AC source of frequency `(200/pi)` Hz and a DC source are applied across the coil.
| AC Source | ||
| S.No. | V (volts) | I (A) |
| 1 | 3.0 | 0.5 |
| 2 | 6.0 | 1.0 |
| 3 | 9.0 | 1.5 |
| DC Source | ||
| S.No. | V (volts) | I (A) |
| 1 | 4.0 | 1.0 |
| 2 | 6.0 | 1.5 |
| 3 | 8.0 | 2.0 |
State the factors on which the magnetic coupling coefficient of two coils depends.
Obtain an expression for the self inductance of a solenoid.
