Advertisements
Advertisements
Question
A container of volume 50 cc contains air (mean molecular weight = 28.8 g) and is open to atmosphere where the pressure is 100 kPa. The container is kept in a bath containing melting ice (0°C). (a) Find the mass of the air in the container when thermal equilibrium is reached. (b) The container is now placed in another bath containing boiling water (100°C). Find the mass of air in the container. (c) The container is now closed and placed in the melting-ice bath. Find the pressure of the air when thermal equilibrium is reached.
Use R = 8.3 J K-1 mol-1
Solution
(a) Here ,
`V_1= 5×10^(-5) "m"^3`
`P_1=10^5 "Pa"`
`T_1 = 273K`
M = 28.8 g
`P_1 V_1 = nRT_1`
⇒ `n =( P_1 V_1)/(RT_1)`
⇒ `m/M = (10^5×5×10^-5)/(8.3×273)`
⇒ `m = (10^5×5×10^-5×28.8)/(8.3×273)`
⇒ m = 0.0635 g
(b) Here,
`V_1 = 5×10^-5 "m"^3`
`P_1 = 10^5 "Pa"`
`P_2 = 10^5 "Pa"`
`T_1 = 273"K"`
`T_2 = 373"K"`
M = 28.8 g
`(P_1 V_1)/(T_1) = (P_2 V_2)/T_2`
`⇒ (5×10^-5)/273` = `V_2/373`
`⇒ V_2 = (5×10^-5×373)/273`
`⇒ V_2 = 6.831×10^-5`
Volume of expelled air `= 6.831×10^-5-5×10^-5`
=`1.831 ×10^-5`
Applying equation of state , we get
PV = nRT
`rArr m/M = (PV)/(RT)= (10^5×1.831×10^-5)/(8.3×373)`
`rArrm = (28.8×10^5×1.831×10^-5)/(8.3×373)=0.017`
Thus, mass of expelled air = 0.017 g
Amount of air in the container = 0.0635 - 0.017 = 0.0465 g
(c) Here,
T = 273K
`P = 10^5 `Pa
`V = 5×10^-5 "m"^3`
Applying equation of state, we get
PV = nRT
`⇒ P = (nRT)/"V" = (0.0465×8.3×273)/(28.8×5×10^-5)`
`P = 0.731×10^5 ≈ 73 "KPa"`
APPEARS IN
RELATED QUESTIONS
A gas is kept in a rigid cubical container. If a load of 10 kg is put on the top of the container, does the pressure increase?
Explain why cooking is faster in a pressure cooker.
A gas behaves more closely as an ideal gas at
Figure shows graphs of pressure vs density for an ideal gas at two temperatures T1 and T2.
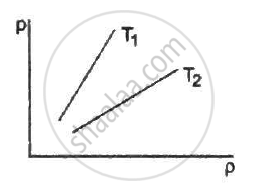
The pressure of a gas kept in an isothermal container is 200 kPa. If half the gas is removed from it, the pressure will be
Equal masses of air are sealed in two vessels, one of volume V0 and the other of volume 2V0. If the first vessel is maintained at a temperature 300 K and the other at 600 K, find the ratio of the pressures in the two vessels.
Use R = 8.31 JK-1 mol-1
Figure shows a cylindrical tube with adiabatic walls and fitted with a diathermic separator. The separator can be slid in the tube by an external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.
Use R=8.314J K-1 mol-1

An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m−3.
In an adiabatic process on a gas with γ = 1.4, the pressure is increased by 0.5%. The volume decreases by about
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg. The length of the gas column in the vessel is 20 cm. The atmospheric pressure is 100 kPa. The vessel is now taken into a spaceship revolving round the earth as a satellite. The air pressure in the spaceship is maintained at 100 kPa. Find the length of the gas column in the cylinder.
Use R = 8.3 J K-1 mol-1
The human body has an average temperature of 98°F. Assume that the vapour pressure of the blood in the veins behaves like that of pure water. Find the minimum atmospheric pressure which is necessary to prevent the blood from boiling. Use figure for the vapour pressures.

A faulty barometer contains certain amount of air and saturated water vapour. It reads 74.0 cm when the atmospheric pressure is 76.0 cm of mercury and reads 72.10 cm when the atmospheric pressure is 74.0 cm of mercury. Saturation vapour pressure at the air temperature = 1.0 cm of mercury. Find the length of the barometer tube above the mercury level in the reservoir.
On a winter day, the outside temperature is 0°C and relative humidity 40%. The air from outside comes into a room and is heated to 20°C. What is the relative humidity in the room? The saturation vapour pressure at 0°C is 4.6 mm of mercury and at 20°C it is 18 mm of mercury.
A bucket full of water is placed in a room at 15°C with initial relative humidity 40%. The volume of the room is 50 m3. (a) How much water will evaporate? (b) If the room temperature is increased by 5°C, how much more water will evaporate? The saturation vapour pressure of water at 15°C and 20°C are 1.6 kPa and 2.4 kPa respectively.
Use R = 8.3 J K-1 mol-1
A cuboidal container having dimensions 2 m × 1.5 m × 0.5 m holds a mixture of 12 g of He, 36 g of Ar, and 20 g of Ne, If the container is maintained at 300 K, Find the pressure exerted by the mixture (given MHe = 4, MAr = 40, MNe = 20).
If 1022 gas molecules each of mass 10-26 kg collide with a surface (perpendicular to it) elastically per second over an area of 1 m2 with a speed of 104 m/s, the pressure exerted by the gas molecules will be of the order of ______.
In a cubical box of volume V, there are N molecules of a gas moving randomly. If m is mass of each molecule and v2 is the mean square of x component of the velocity of molecules, then the pressure of the gas is ______.
