Advertisements
Advertisements
Question
A current of 1.0 A is established in a tightly wound solenoid of radius 2 cm having 1000 turns/metre. Find the magnetic energy stored in each metre of the solenoid.
Solution
Given:-
Current through the solenoid, i = 1.0 A
Radius of the coil, r = 2 cm
Number of turns per metre, n = 1000
The magnetic energy density is given by \[\frac{B^2}{2 \mu_0}.\]
Volume of the solenoid, V = πr2l
For l = 1m, V = πr2
Thus, the magnetic energy stored in volume V is given by
\[U=\frac{B^2 \pi r^2}{2 \mu_0}\]
The magnetic field is given by
B = μ0ni
= (4π × 10-7) × (1000) × 1
= 4π × 10-4 Τ
\[U = \frac{(4\pi \times {10}^{- 4} )^2 \times 4\pi \times {10}^{- 4}}{2 \times (4\pi \times {10}^{- 7} )} \]
\[ = 8 \pi^2 \times {10}^{- 5} \]
\[ = 78 . 956 \times {10}^{- 5} \]
\[ = 7 . 9 \times {10}^{- 4} J\]
APPEARS IN
RELATED QUESTIONS
Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius 'r', having 'n' turns per unit length and carrying a steady current I.
An observer to the left of a solenoid of N turns each of cross section area 'A' observes that a steady current I in it flows in the clockwise direction. Depict the magnetic field lines due to the solenoid specifying its polarity and show that it acts as a bar magnet of magnetic moment m = NIA.
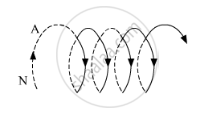
Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow thought the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system
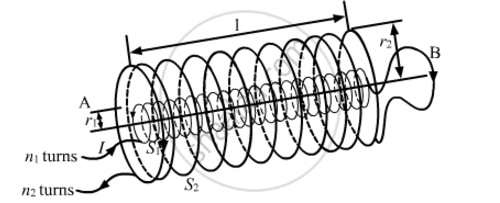
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2, respectively.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
A magnetic field of 100 G (1 G = 10−4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10−3 m2. The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m−1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Define self-inductance of a coil.
In what respect is a toroid different from a solenoid?
Draw and compare the pattern of the magnetic field lines in the two cases ?
A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
A tightly-wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current i n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) verify that if l >> a, the field tends to B = µ0ni and if a >> l, the field tends to `B =(mu_0nil)/(2a)` . Interpret these results.
A tightly-wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surface current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) Find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
A capacitor of capacitance 100 µF is connected to a battery of 20 volts for a long time and then disconnected from it. It is now connected across a long solenoid having 4000 turns per metre. It is found that the potential difference across the capacitor drops to 90% of its maximum value in 2.0 seconds. Estimate the average magnetic field produced at the centre of the solenoid during this period.
The length of a solenoid is 0.4 m and the number turns in it is 500. A current of 3 amp, is flowing in it. In a small coil of radius 0.01 m and number of turns 10, a current of 0.4 amp. is flowing. The torque necessary to keep the axis of this coil perpendicular to the axis of solenoid will be ______.
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to ______.
