Advertisements
Advertisements
Question
A dipole with its charges, - q and + q located at the points (O, -b, O) and (O, +b, O) is present in a uniform electric field E. The equipotential surfaces of this field are planes parallel to the yz plane.
(a) What is the direction of the electric field E?
(b) How much torque would the dipole experience in this field?
Solution
(a) Given, the equipotentials of the external uniform electric field are planes parallel to the yz plane, the electric field `vec "E" = +- "E" hat"i"` that is, `vec "E"` is parallel to the x-axis.
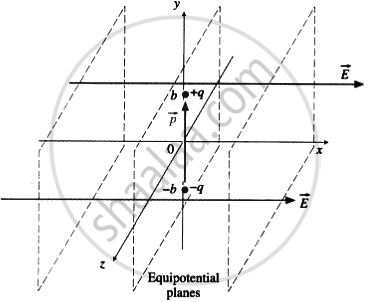
A dipole in an external electric field along x-axis
(b) The above diagram, the dipole moment, `vec"p" = "q"(2"b") hat"j"`
The torque on this dipole,
`vec τ = vec"p" xx vec "E" = (2 "qb"hat"j") xx (+- "E"hat"i") = (2"qbE")(hat"j" xx hat "i")`
Since `hat"j" xx hat "i" = - bar"k"`
`vec τ = (+- 2"qbE")(-hat"k") = (2"qbE")(+- hat"k")`
So that the magnitude of the torque is τ = 2qbE.
If `vec"E"` is in the direction of the + x-axis, the torque `vec τ` is in the direction of - z-axis, while if `vec "E"` s in the direction of the - x-axis, the torque `vec tau` is in the direction of + z-axis.
RELATED QUESTIONS
Answer in brief:
A charge q is moved from a point A above a dipole of dipole moment p to a point B below the dipole in an equatorial plane without acceleration. Find the work done in this process.
Three charges –q, +Q, and –q are placed at equal distances on a straight line. If the potential energy of the system of the three charges is zero, then what is the ratio of Q: q?
Electric potential due to the system of charges is calculated using the principle of ______
Derive an expression for the electric potential at a point due to a short electric dipole. Hence, write the expression for the electric potential at a point (i) dipole axis and (ii) on the dipole equator.
The work done in bringing a unit positive charge from infinity to a given point against the direction of electric field is known as ______.
