Advertisements
Advertisements
Question
A football player hits the ball with a speed of 20 m s-1 with an angle of 30° with respect to horizontal direction as shown in the figure. The goal post is at a distance of 40 m from him. Find out whether the ball reaches the goal post?
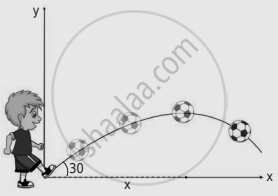
Solution
Given:
Initial speed (u) = 20 ms-1
The angle of projection (θ) = 30°
The distance of the goal post = 40 m
Solution:
Range of the projectile R = `(u^2 sin2theta)/g = (400 xx sin 60^circ)/9.8 = (400 xx sqrt3/2)/9.8` = 35.35 m
The distance of the goal post is 40 m. But the range of the ball is 35.35 m only. So the ball will not reach the goal post.
APPEARS IN
RELATED QUESTIONS
Two objects are projected at angles 30° and 60° respectively with respect to the horizontal direction. The range of two objects is denoted as R30° and R60°. Choose the correct relation from the following.
Define a radian?
Define angular displacement.
An object at an angle such that the horizontal range is 4 times the maximum height. What is the angle of projection of the object?
An object of mass m has angular acceleration α = 0.2 rad s-2. What is the angular displacement covered by the object after 3 seconds? (Assume that the object started with angle zero with zero angular velocity).
An object is executing uniform circular motion with an angular speed of `pi/12` radians per second. At t = 0 the object starts at an angle θ = 0 What is the angular displacement of the particle after 4 s?
If an object is thrown horizontally with an initial speed of 10 ms -1 from the top of a building of height 100 m. What is the horizontal distance covered by the particle?
An object is thrown with an initial speed of 5 m s-1 with an angle of projection of 30°. What is the height and range reached by the particle?
If Earth completes one revolution in 24 hours, what is the angular displacement made by Earth in one hour? Express your answer in both radian and degree.
