Advertisements
Advertisements
Question
A. hot solid of mass 60 g at 100°C is placed in 150 g of water at 20° C. The final steady temperature recorded is 25°C. Calculate the specific heat capacity of the solid. [Specific heat capacity of water = 4200 J kg-1 °C-1]
Solution
Mass of hot solid m = 60 gm, at 100 C
Mass of water, m2 = 150 gm, at 20 C
Final temperature = 25 C
By principle of calorimetry,
Heat given = Heat taken
⇒ m1c1ΔQ1 = m2c2ΔQ2
⇒ 60 × c × (100 - 25) = 150 × 4.2 × (25 - 20)
⇒ ∴ Required specific heat, c1 = 0.7 J/ gm °C
APPEARS IN
RELATED QUESTIONS
In an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150 °C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27 °C. The final temperature is 40 °C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for the specific heat of the metal?
Calculate the mass of ice needed to cool 150 g of water contained in a calorimeter of mass 50 g at 32 °C such that the final temperature is 5 °C. Specific heat capacity of calorimeter = 0.4 J g-1 °C-1, Specific heat capacity of water = 4.2 J g-1°C-1, latent heat capacity of ice = 330 J g-1.
Calculate the mass of ice required to lower the temperature of 300 g of water 40°C to water at 0°C.
(Specific latent heat of ice = 336 J/g, the Specific heat capacity of water = 4.2J/g°C)
What is the specific heat capacity of boiling water?
A substance is heated at a constant rate from a low temperature to a high temperature. A graph of temperature against time is shown in the figure. Which part or parts of the graph correspond(s) to the substance existing in two states?
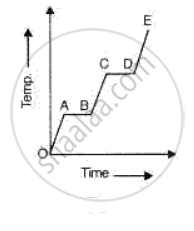
63.2 g of copper at 50°C can just melt 3.8g of ice. If the specific latent heat of ice is 336 J/g, find the specific heat capacity of copper.
The ratio of the specific heats `c_"p"/c_"v"=gamma` in terms of degrees of freedom 'n' is given by ______.
Two metals A and B have specific heat capacities in the ratio 2 : 3. If they are supplied the same amount of heat then
Which metal piece will show a greater rise in temperature given their masses is the same?
We would like to make a vessel whose volume does not change with temperature (take a hint from the problem above). We can use brass and iron `(β_(vbrass) = (6 xx 10^(–5))/K and β_(viron) = (3.55 xx 10^(–5))/K)` to create a volume of 100 cc. How do you think you can achieve this.
