Advertisements
Advertisements
Question
A lens forms the image of an object placed at a distance 15 cm from it, at a distance 60 cm in front of it. Find the focal length.
Solution
Object distance, u = -15 cm
Image distance, v = -60 cm
Lens formula is,
`1/v - 1/u = 1/f`
∴ `1/-60 - 1/-15 = 1/f`
∴ `1/f = 1/15 - 1/60`
∴ `1/f = 3/60`
∴ `1/f = 1/20`
∴ f = 20 cm
APPEARS IN
RELATED QUESTIONS
Describe in brief how would you determine the approximate focal length of a convex lens.
The following diagram shows the experimental set up for the determination of focal length of a lens using a plane mirror.
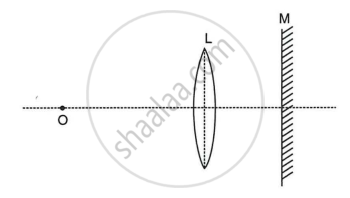
- Draw two rays from the point O of the object to show the formation of image I at O itself.
- What is the size of the image I?
- State two more characteristics of the image I.
- Name the distance of the objects O from the optical centre of the lens.
- To what point will the rays return if the mirror is moved away from the lens by a distance equal to the focal length of the lens?
A convex lens forms an inverted image of size same as that of the object which is placed at a distance 60 cm in front of the lens. Find:
- The position of the image, and
- The focal length of the lens.
A concave lens forms an erect image of `1/3`rd the size of the object which is placed at a distance 30 cm in front of the lens. Find:
- the position of image, and
- the focal length of the lens.
The focal length of a convex lens is 25 cm. Express its power with sign.
The power of a lens is -2.0 D. Find its focal length and its kind.
Describe how you would determine the focal length of a converging lens, using a plane mirror and one pin. Draw a ray diagram to illustrate your answer.
