Advertisements
Advertisements
Question
A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10 sq.units
Solution
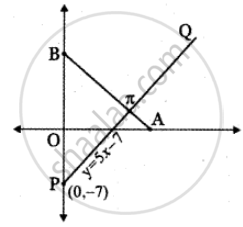
Let the given line be PQ whose equation is
5x = y + 7
5x – y – 7 = 0 ......(1)
Let AB be the line perpendicular to the line PQ such that the area of the triangle OAB is 10 units.
The equation of the line AB is
– x – 5y + k = 0
x + 5y – k = 0
x + 5y = k ......(2)
`x/"l" + (5y)/"k"` = 1
`x/"k" + y/("k"/5)` = 1
∴ A is (k, 0) and B is `(0, "k"/5)`
OA = k and OB = `"k"/5`
Area of ∆OAB = `1/2 xx "OA" xx "OB"`
= `1/2 xx "k" xx "k"/5`
Given area of ∆OAB = 10
∴ `("k"^2)/10` = 10
k2 = 100
⇒ k = ±10
∴ The required equation of the straight line is
x + 5y = ±10
APPEARS IN
RELATED QUESTIONS
Find the distance between the line 4x + 3y + 4 = 0, and a point (−2, 4)
Write the equation of the lines through the point (1, −1) parallel to x + 3y − 4 = 0
Write the equation of the lines through the point (1, −1) perpendicular to 3x + 4y = 6
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and through the point (−1, 2)
Find the equations of two straight lines which are parallel to the line 12x + 5y + 2 = 0 and at a unit distance from the point (1, −1)
Find the equations of straight lines which are perpendicular to the line 3x + 4y − 6 = 0 and are at a distance of 4 units from (2, 1)
Find the equation of a straight line parallel to 2x + 3y = 10 and which is such that the sum of its intercepts on the axes is 15
Find the length of the perpendicular and the co-ordinates of the foot of the perpendicular from (−10, −2) to the line x + y − 2 = 0
If p1 and p2 are the lengths of the perpendiculars from the origin to the straight lines x sec θ + y cosec θ = 2a and x cos θ – y sin θ = a cos 2θ, then prove that p12 + p22 = a2
Find the distance between the parallel lines
12x + 5y = 7 and 12x + 5y + 7 = 0
Find the family of straight lines perpendicular
A photocopy store charges ₹ 1.50 per copy for the first 10 copies and ₹ 1.00 per copy after the 10th copy. Let x be the number of copies, and let y be the total cost of photocopying. Find the cost of making 40 copies
Find all the equations of the straight lines in the family of the lines y = mx − 3, for which m and the x-coordinate of the point of intersection of the lines with x − y = 6 are integers
Choose the correct alternative:
If the two straight lines x + (2k − 7)y + 3 = 0 and 3kx + 9y − 5 = 0 are perpendicular then the value of k is
Choose the correct alternative:
If the lines represented by the equation 6x2 + 41xy – 7y2 = 0 make angles α and β with x-axis then tan α tan β =
Choose the correct alternative:
θ is acute angle between the lines x2 – xy – 6y2 = 0 then `(2costheta + 3sintheta)/(4costheta + 5costheta)`
