Question

A line passing through (4, – 2) and intersects the Y-axis at (0, 2). Find a point on the line in the second quadrant

Answer 1

A line passes through (4, – 2)

y-axis intercept point – (0, 2)

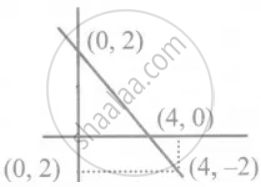
Using the point formula

`(y - y_1)/(x - x_1) = (y_2 - y_1)/(x_2 - x_1)`

`(y - 2)/(x - 0) = (-2 - 2)/(4 - 0)`

∴ `(y - 2)/x = (-4)/4` = −1

y − 2 = −1 × x

∴ y − 2 = −x

∴ x + y = 2 is the equation of the line.
Any point in II quadrant will have x as negative & y as positive.

So let us take x value as – 2

∴ −2 + y = 2

∴ y = 2 + 2 = 4

∴ Point in II Quadrant is (−2, 4)