Question

A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r (Figure).

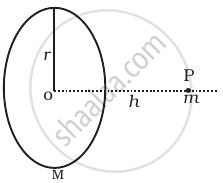
If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h=r?

Answer 1

Consider the diagram in which a system consisting of a ring and a point mass is shown.

The gravitational force acting on an object of mass m, placed at point P at a distance h along the normal through the centre of a circular ring of mass M and radius r is given by

`F = (GMmh)/(r^2 + h^2)^(3/2)`  (along PO)  ......(i)

When the mass is displaced up to a distance 2h, then

`F^' = (GMm xx 2h)/([r^2 + (2h)^2]^(3/2)`  .....[∵ h = 2r]

= `(2GMh)/(r^2 + 4h^2)^(3/2)`  ......(ii)

When h = r, then from equation (i)

`F = (GMm xx r)/(r^2 + r^2)^(3/2)`

⇒ `F = (GMm)/(2sqrt(2r^2)`

And `F^' = (2GMmr)/(r^2 + 4r^2)^(3/2) = (2GMm)/(5sqrt(5r^2))`  .......[From equation (i) substituting h = r]

∴ `F^'/F = (4sqrt(2))/(5sqrt(5))`

⇒ `F^' = (4sqrt(2))/(5sqrt(5)) F`