Advertisements
Advertisements
Question
A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum l. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease.
Advertisements
Solution
The situation is shown in the diagram, where a body of mass m is revolving around a star of mass M.
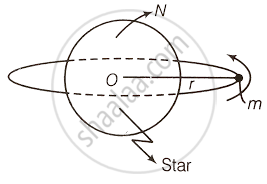
Linear velocity of the body `v = sqrt((GM)/r)`
⇒ `v ∝ 1/sqrt(r)`
Therefore, when r increases, v decreases.
Angular velocity of the body `ω = (2π)/T`
According to Kepler's law of the period,
`T^2 ∝ r^3` ⇒ `T = kr^(3/2)`
Where k is a constant
∴ `ω = (2π)/(kr^(3/2))` ⇒ `ω ∝ 1/r^(3/2)` .....`(∵ ω = (2π)/T)`
Therefore, when r increases, ω decreases.
The kinetic energy of the body,
K = `1/2 mv^2`
= `1/2 m xx (GM)/r`
= `(GMm)/(2r)`
∴ `K ∝ 1/r`
Therefore, when r increases, KE decreases.
The gravitational potential energy of the body,
`U = - (GMm)/r` ⇒ `U ∝ 1/r`
Therefore, when r increases, PE becomes less negative i.e., increases.
Total energy of the body,
`E = KE + PE`
= `(GMm)/(2r) + (- (GMm)/r)`
= `- (GMm)/(2r)`
Therefore, when r increases, total energy becomes less negative, i.e., increases.
Angular momentum of the body,
`L = mvr`
= `mr sqrt((GM)/r)`
= `msqrt(GMr)`
∴ `L ∝ sqrt(r)`
Therefore, when r increases, angular momentum L increases.
APPEARS IN
RELATED QUESTIONS
State Kepler's law of orbit and law of equal areas.
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be \[\sqrt{8}\] T.
Identify the law shown in the figure and state three respective laws.
In the Following figure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively,
Observe the given figure showing the orbit of a planet moving around the Sun and write the three laws related to it:
The orbit of a planet moving around the Sun
The square of its period of revolution around the sun is directly proportional to the ______ of the mean distance of a planet from the sun.
The third law of Kepler is also known as the Law of ______.
State Kepler’s laws.
The mass and radius of earth is 'Me' and 'Re' respectively and that of moon is 'Mm' and 'Rm' respectively. The distance between the centre of the earth and that of moon is 'D'. The minimum speed required for a body (mass 'm') to project from a point midway between their centres to escape to infinity is ______.
The earth moves around the sun in an elliptical orbit as shown in the figure. The ratio, `"OA"/"OB"` = x. The ratio of the speed of the earth at Band at A is ______.
A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b, then the time period is given by:
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon ______.
In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They ______.
Supposing Newton’s law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F1 = – F2 = `- r_12/r_12^3 GM_0^2 ((m_1m_2)/M_0^2)^n` where M0 is a constant of dimension of mass r12 = r1 – r2 and n is a number. in such a case.
- the acceleration due to gravity on earth will be different for different objects.
- none of the three laws of Kepler will be valid.
- only the third law will become invalid.
- for n negative, an object lighter than water will sink in water.
The centre of mass of an extended body on the surface of the earth and its centre of gravity ______.
- are always at the same point for any size of the body.
- are always at the same point only for spherical bodies.
- can never be at the same point.
- is close to each other for objects, say of sizes less than 100 m.
- both can change if the object is taken deep inside the earth.
Draw areal velocity versus time graph for mars.
The maximum and minimum distances of a comet from the Sun are 1.6 × 1012 m and 8.0 × 1010 m respectively. If the speed of the comet at the nearest point is 6 × 104 ms-1, the speed at the farthest point is ______.
What is at one focus of the elliptical orbit of a planet?
