Advertisements
Advertisements
Question
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Advertisements
Solution
Consider the diagram below, in which six point masses are placed at six verticles A, B, C, D, E and F.
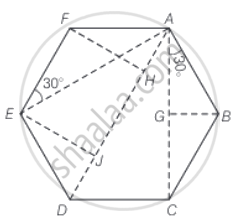
AC = AG + GC = 2AG
= `2l cos 30^circ`
= `2l sqrt(3)/2`
= `sqrt(3)l`
= AE
AD = AH + HJ + JD
= `l sin 30^circ + l + l sin 30^circ`
= `2l`
Force on mass m at A due to mass m at B is, `f_1 = (Gmm)/l^2` = along AB.
Force on mass m at A due to mass m at C is, `f_2 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AC. ......[∵ AC = `sqrt(2)`l]
Force on mass m at A due to mass m at D is, `f_3 = (Gm xx m)/(2l)^2 = (Gm^2)/(4l^2)` along AD ......[∵ AD = 2l]
Force on mass m at A due to mass m at E is, `f_4 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AE.
Force on mass m at A due to mass m at F is, `f_5 = (Gm xx m)/l^2 = (Gm^2)/l^2`along AF.
Resultant force due to `f_1` and `f_5` is `F_1 = sqrt(f_1^2 + f_5^2 + 2f_1f_5 cos 120^circ) = (Gm^2)/l^2` along AD. ...........[∵ Angle between `f_1` and `f_2` = 120°]
Resultant force due to `f_2` and `f_4` is `F_2 = sqrt(f_2^2 + f_4^2 + 2f_2f_4 cos 60^circ) = (sqrt(3)Gm^2)/(3l^2) = (Gm^2)/(sqrt(3)l^2)`along AD.
So, net force along AD = `F_1 + F_2 + F_3`
= `(Gm^2)/l^2 + (Gm^2)/(sqrt(3)l^2) + (Gm^2)/(4l^2)`
= `(Gm^2)/l^2 (1 + 1/sqrt(3) + 1/4)`
APPEARS IN
RELATED QUESTIONS
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Choose the correct alternative:
Acceleration due to gravity is independent of mass of the earth/mass of the body.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
State two applications of universal law of gravitation.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
The mass of moon is about 0.012 times that of earth and its diameter is about 0.25 times that of earth. The value of G on the moon will be:
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
A ball is thrown up with a speed of 4.9 ms-1.
Prove that the time of ascent is equal to the time of descent.
What is meant by the equation :
`g= Gxxm/r^2`
where the symbols have their usual meanings.
Name and state the action and reaction in the following case:
Hammering a nail.
What is the difference between gravity and gravitation?
Explain why:
The atmosphere does not escape.
Explain the difference between g and G.
The _______ force is much weaker than other forces in nature.
Give the applications of universal law gravitation.
As observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from earth, this would ______.
Give scientific reasons for the following:
Newton's gravitational law is the universal law of gravitation.
