Question

A satellite is to be placed in equatorial geostationary orbit around earth for communication.

1. Calculate height of such a satellite.
2. Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.

[M = 6 × 10²⁴ kg, R = 6400 km, T = 24 h, G = 6.67 × 10^–11 SI units]

Answer 1

Consider the adjacent diagram

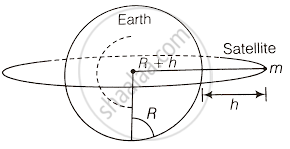
Given, the mass of the earth M = 6 × 10²⁴ kg

The radius of the earth, R = 6400 km = 6.4 × 10⁶ m

Time period T = 24 h

= 24 × 60 × 60

= 86400 s

G = 6.67 × 10^–11 N-m²/kg²

a. Time period T = `2πsqrt((R + h)^3/(GM))`  ......`[∵ v_0 = sqrt((GM)/(R + h)) and T = (2π(R + h))/v_0]`

⇒ `T^2 = 4π^2 (R + h)^3/(GM)`

⇒ `(R + h)^3 = (T^2GM)/(4π^2)`

⇒ `R + h = ((T^2GM)/(4π^2))^(1/3)`

⇒ `h = ((T^2GM)/(4π^2))^(1/3) - R`

⇒ `h = [((24 xx 60 xx 60)^2 xx 6.67 xx 10^-11 xx 6 xx 10^24)/(4 xx (3.14)^2)]^(1/3) - 6.4 xx 10^6`

= `4.23 xx 10^7 - 6.4 xx 10^6`

= `(42.3 - 6.4) xx 10^6`

= `35.9 xx 10^6` m

= 3.59 × 10⁷ m

b. If the satellite is at height h from the earth's surface, then according to the diagram.

 

`cos theta = R/(R + h)`

= `1/((1 + h/R))`

= `1/((1 + (3.59 xx 10^7)/(6.4 xx 10^6))`

= `1/(1 + 5.61)`

= `1/6.61`

= 0.513

= cos 81°18'

θ = 81°18'

∴  2θ = 2 × (81°18') = 162°36'

If n is the number of satellites needed to cover entire the earth, then

n = `360^circ/(2θ) = 360^circ/(162^circ36^')` = 2.31

∴ Minimum 3 satellites are required to cover entire the earth.