Question

Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.

Answer 1

Consider the diagram below, in which six point masses are placed at six verticles A, B, C, D, E and F.

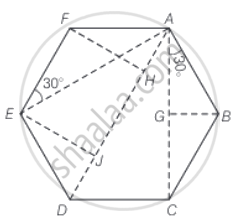
AC = AG + GC = 2AG

= `2l cos 30^circ`

= `2l sqrt(3)/2`

= `sqrt(3)l`

= AE

AD = AH + HJ + JD

= `l sin 30^circ +  l + l sin 30^circ`

= `2l`

Force on mass m at A due to mass m at B is, `f_1 = (Gmm)/l^2` = along AB.

Force on mass m at A due to mass m at C is, `f_2 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AC.  ......[∵ AC = `sqrt(2)`l]

Force on mass m at A due to mass m at D is, `f_3 = (Gm xx m)/(2l)^2 = (Gm^2)/(4l^2)` along AD   ......[∵ AD = 2l]

Force on mass m at A due to mass m at E is, `f_4 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AE.

Force on mass m at A due to mass m at F is, `f_5 = (Gm xx m)/l^2 = (Gm^2)/l^2`along AF.

Resultant force due to `f_1` and `f_5` is `F_1 = sqrt(f_1^2 + f_5^2 + 2f_1f_5 cos 120^circ) = (Gm^2)/l^2` along AD.  ...........[∵ Angle between `f_1` and `f_2` = 120°]

Resultant force due to `f_2` and `f_4` is `F_2 = sqrt(f_2^2 + f_4^2 + 2f_2f_4 cos 60^circ) = (sqrt(3)Gm^2)/(3l^2) = (Gm^2)/(sqrt(3)l^2)`along AD.

So, net force along AD = `F_1 + F_2 + F_3`

= `(Gm^2)/l^2 + (Gm^2)/(sqrt(3)l^2) + (Gm^2)/(4l^2)`

= `(Gm^2)/l^2 (1 + 1/sqrt(3) + 1/4)`