Advertisements
Advertisements
प्रश्न
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
उत्तर
Consider the diagram below, in which six point masses are placed at six verticles A, B, C, D, E and F.
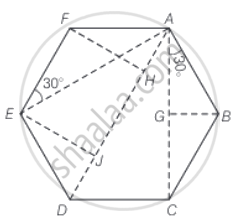
AC = AG + GC = 2AG
= `2l cos 30^circ`
= `2l sqrt(3)/2`
= `sqrt(3)l`
= AE
AD = AH + HJ + JD
= `l sin 30^circ + l + l sin 30^circ`
= `2l`
Force on mass m at A due to mass m at B is, `f_1 = (Gmm)/l^2` = along AB.
Force on mass m at A due to mass m at C is, `f_2 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AC. ......[∵ AC = `sqrt(2)`l]
Force on mass m at A due to mass m at D is, `f_3 = (Gm xx m)/(2l)^2 = (Gm^2)/(4l^2)` along AD ......[∵ AD = 2l]
Force on mass m at A due to mass m at E is, `f_4 = (Gm xx m)/(sqrt(3)l)^2 = (Gm^2)/(3l^2)` along AE.
Force on mass m at A due to mass m at F is, `f_5 = (Gm xx m)/l^2 = (Gm^2)/l^2`along AF.
Resultant force due to `f_1` and `f_5` is `F_1 = sqrt(f_1^2 + f_5^2 + 2f_1f_5 cos 120^circ) = (Gm^2)/l^2` along AD. ...........[∵ Angle between `f_1` and `f_2` = 120°]
Resultant force due to `f_2` and `f_4` is `F_2 = sqrt(f_2^2 + f_4^2 + 2f_2f_4 cos 60^circ) = (sqrt(3)Gm^2)/(3l^2) = (Gm^2)/(sqrt(3)l^2)`along AD.
So, net force along AD = `F_1 + F_2 + F_3`
= `(Gm^2)/l^2 + (Gm^2)/(sqrt(3)l^2) + (Gm^2)/(4l^2)`
= `(Gm^2)/l^2 (1 + 1/sqrt(3) + 1/4)`
APPEARS IN
संबंधित प्रश्न
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
Multiple Choice Question. Select the correct option.
The mass of earth is 6 × 1024 kg and radius of earth is 6.4 × 106 m. The magnitude of force between the mass of 1 kg and the earth is:
Is the law of gravitation applicable in case of the sun and the moon?
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
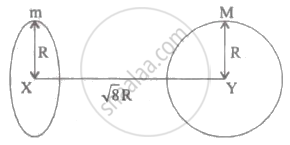
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.