Question

Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.

Answer 1

Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = \[\sqrt{2}a\]

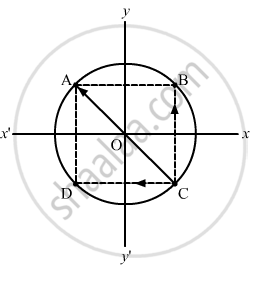
The force on the particle at C due to gravitational attraction of the particle at B is

\[\overrightarrow{F}_{CB} = \frac{G M^2}{2 R^2} \hat j\] .

The force on the particle at C due to gravitational attraction of the particle at D is

\[\overrightarrow{F}_{CD} = - \frac{G M^2}{2 R^2} \hat i\].

Now, force on the particle at C due to gravitational attraction of the particle at A is given by

\[\overrightarrow{F}_{CA} = - \frac{G M^2}{4 R^2}\cos 45 \hat i + \frac{G M^2}{4 R^2}\sin 45 \hat j\]

\[ \therefore \overrightarrow{F}_C = \overrightarrow{F}_{CA} + \overrightarrow{F}_{CB} + \overrightarrow{F}_{CD} \]

\[ = \frac{- G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat i + \frac{G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat j\]

So, the resultant gravitational force on C is \[F_C = \frac{G m^2}{4 R^2}\sqrt{2\sqrt{2} + 1}\]

Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by

\[F = \frac{m v^2}{R}\]

\[ \Rightarrow v = \sqrt{\frac{GM}{R}\left( \frac{2\sqrt{2} + 1}{4} \right)}\]