Advertisements
Advertisements
प्रश्न
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Advertisements
उत्तर
Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = \[\sqrt{2}a\]
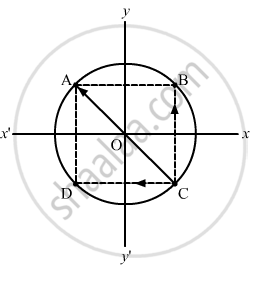
The force on the particle at C due to gravitational attraction of the particle at B is
\[\overrightarrow{F}_{CB} = \frac{G M^2}{2 R^2} \hat j\] .
The force on the particle at C due to gravitational attraction of the particle at D is
\[\overrightarrow{F}_{CD} = - \frac{G M^2}{2 R^2} \hat i\].
Now, force on the particle at C due to gravitational attraction of the particle at A is given by
\[\overrightarrow{F}_{CA} = - \frac{G M^2}{4 R^2}\cos 45 \hat i + \frac{G M^2}{4 R^2}\sin 45 \hat j\]
\[ \therefore \overrightarrow{F}_C = \overrightarrow{F}_{CA} + \overrightarrow{F}_{CB} + \overrightarrow{F}_{CD} \]
\[ = \frac{- G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat i + \frac{G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat j\]
So, the resultant gravitational force on C is \[F_C = \frac{G m^2}{4 R^2}\sqrt{2\sqrt{2} + 1}\]
Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by
\[F = \frac{m v^2}{R}\]
\[ \Rightarrow v = \sqrt{\frac{GM}{R}\left( \frac{2\sqrt{2} + 1}{4} \right)}\]
APPEARS IN
संबंधित प्रश्न
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
If the moon attracts the earth, why does the earth not move towards the moon?
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing altitude.
State the universal law of gravitation. Name the scientist who gave this law.
State whether the gravitational force between two masses is attractive or repulsive ?
Who stated the law of gravitation?
What does a force do in the following case?
You pull the skin of your arm
What does a force do in the following case?
You catch a kicked ball.
Name and state the action and reaction in the following case:
A person walking on the ground.
Two equal and opposite forces acting at the same point on a stationary body. Will the body move? Give reason to explain your answer.
Gravity is another kind of ________. It exerts all through the ________. The Sun's gravity keeps the ___________ in their orbits. Gravity can only be felt with very large ________.
Explain the difference between g and G.
State Newton’s universal law of gravitation. Express it with the mathematical form of force of gravitation?
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Shown are several curves (Figure). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
