Advertisements
Advertisements
प्रश्न
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
उत्तर
Consider that mass m is at a distance \[\frac{R_1 + R_2}{2}\] as shown in the figure.
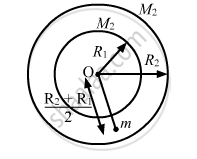
The gravitational force of m due to the shell of M2 is zero, because the mass is inside the shell.
∴ Gravitational force due to the shell of mass M2 = \[\frac{G M_1 m}{\left( \frac{R_1 + R_2}{2} \right)^2} = \frac{4G M_1 m}{\left( R_1 + R_2 \right)^2}\]
APPEARS IN
संबंधित प्रश्न
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
State two applications of universal law of gravitation.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements :
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Define one Newton. How much maximum acceleration can it produce in a mass of 1 kg?
Distinguish between gravity and gravitation
What does a force do in the following case?
You twist a piece of rubber.
What does a force do in the following case?
You catch a kicked ball.
Explain why:
The atmosphere does not escape.
Is there a gravitational attraction between you and the book? Explain.
Answer the following question.
State Newton’s law of gravitation and express it in vector form.
What do you mean by a gravitational constant?
For the weight of body of mass 5 kg to be zero on equator of the earth, angular velocity of the earth must be (The radius of earth = 6400 km, acceleration due to gravity = 10 m/s2).
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
