Advertisements
Advertisements
Question
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
Solution
Consider that mass m is at a distance \[\frac{R_1 + R_2}{2}\] as shown in the figure.
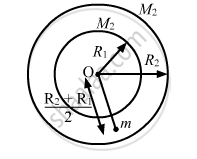
The gravitational force of m due to the shell of M2 is zero, because the mass is inside the shell.
∴ Gravitational force due to the shell of mass M2 = \[\frac{G M_1 m}{\left( \frac{R_1 + R_2}{2} \right)^2} = \frac{4G M_1 m}{\left( R_1 + R_2 \right)^2}\]
APPEARS IN
RELATED QUESTIONS
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Can we apply Newton’s third law to the gravitational force ? Explain your answer.
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Which of the following quantities remain constant in a planetary motion (consider elliptical orbits) as seen from the sun?
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
Define one Newton. How much maximum acceleration can it produce in a mass of 1 kg?
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Infinite
Is there a gravitational attraction between you and the book? Explain.
Answer the following question.
What are the dimensions of the universal gravitational constant?
Choose the wrong option.
