Advertisements
Advertisements
Questions
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Answer the following question.
State Newton’s law of gravitation.
Solution
The universal law of gravitation states that every object in the universe attracts every other object with a force called the gravitational force. The force acting between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
F ∝ m M (masses of two bodies m and M)
F ∝ `1/"d"^2` (d is the distance between the two bodies.)
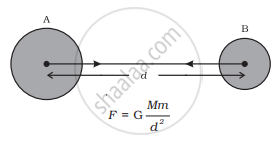
A and B are two bodies, the distance between which is given as d.
F = force with which one body is attracting the other.
G = proportionality constant.
APPEARS IN
RELATED QUESTIONS
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
What happens to the force between two objects, if the distance between the objects is doubled and tripled?
What is the importance of the universal law of gravitation?
Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 1024 kg and of the Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing depth. (assume the earth to be a sphere of uniform density).
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
State Kepler’s law which is represented by the relation r3 ∝ T2.
Can we apply Newton’s third law to the gravitational force ? Explain your answer.
Universal law of gravitation states that every object exerts a gravitational force of attraction on every other object. If this is true, why don’t we notice such forces ? Why don’t the two objects in a room move towards each other due to this force ?
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s −1 as it reaches A. The work done by the person on the mass is −3 J. The potential at A is
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Inside a uniform spherical shell
(a) the gravitational potential is zero
(b) the gravitational field is zero
(c) the gravitational potential is same everywhere
(d) the gravitational field is same everywhere
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
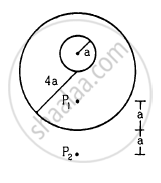
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
The law of gravitation gives the gravitational force between :
Explain the following:
People often shake the branches of a tree for getting down its fruits.
State whether the gravitational force between two masses is attractive or repulsive ?
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
Is the law of gravitation applicable in case of the sun and the moon?
What is meant by the equation :
`g= Gxxm/r^2`
where the symbols have their usual meanings.
What does a force do in the following case?
You pull the skin of your arm
What does a force do in the following case?
You twist a piece of rubber.
What does a force do in the following case?
You apply brakes to a running car.
Name and state the action and reaction in the following case:
A book lying on a table.
Why does a ball moving on a table top eventually stops?
State the law of gravitation. Why is it called universal?
Explain the difference between g and G.
An apple falls towards the earth due to its gravitational force. The apple also attracts the earth with the same force. Why do we not see the earth rising towards the apple? Explain.
The distance-time values for an object moving along straight line are given below:
| Time (s) | Distance (m) |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
Show that gravity decreases at higher altitudes.
Answer the following question.
State Newton’s law of gravitation and express it in vector form.
What do you mean by a gravitational constant?
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
The gravitational force between two bodies is directly proportional to the product of the masses of those bodies and is _______ of the distance between them.
The _______ force is much weaker than other forces in nature.
State Newton's universal law of gravitation. Express it with the mathematical form of force of gravitation?
Different points in earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m. For the earth-sun system (approximating the earth as a uniform density sphere).
How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
Newton's universal law of gravitation applies to ______.
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
Observe the figure and answer the questions:
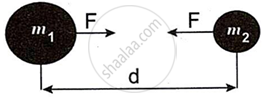
- State Newton's universal law of gravitation.
- If the distance between the two bodies is tripled, how will the gravitational force between them change?
- What will happen to gravitational force, if mass of one of the object is doubled?
