Advertisements
Advertisements
प्रश्न
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Answer the following question.
State Newton’s law of gravitation.
उत्तर
The universal law of gravitation states that every object in the universe attracts every other object with a force called the gravitational force. The force acting between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
F ∝ m M (masses of two bodies m and M)
F ∝ `1/"d"^2` (d is the distance between the two bodies.)
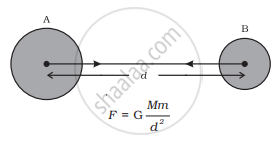
A and B are two bodies, the distance between which is given as d.
F = force with which one body is attracting the other.
G = proportionality constant.
APPEARS IN
संबंधित प्रश्न
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Choose the correct alternative:
Acceleration due to gravity is independent of mass of the earth/mass of the body.
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
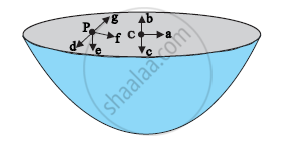
Choose the correct answer from among the given ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Universal law of gravitation states that every object exerts a gravitational force of attraction on every other object. If this is true, why don’t we notice such forces ? Why don’t the two objects in a room move towards each other due to this force ?
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Can you think of two particles which do not exert gravitational force on each other?
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
A person sitting in a chair in a satellite feels weightless because
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
Explain the following:
People often shake the branches of a tree for getting down its fruits.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
Multiple Choice Question. Select the correct option.
The mass of earth is 6 × 1024 kg and radius of earth is 6.4 × 106 m. The magnitude of force between the mass of 1 kg and the earth is:
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Infinite
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
What does a force do in the following case?
You pull the skin of your arm
What does a force do in the following case?
You twist a piece of rubber.
What does a force do in the following case?
You catch a kicked ball.
Name and state the action and reaction in the following case:
A book lying on a table.
Name and state the action and reaction in the following case:
A person walking on the ground.
Why does a ball moving on a table top eventually stops?
Does the force of the earth's gravitation affect the motion of the moon? Explain your answer with reasons.
State Newton's law of gravitation. What is the difference between:
g and G?
An apple falls towards the earth due to its gravitational force. The apple also attracts the earth with the same force. Why do we not see the earth rising towards the apple? Explain.
Show that gravity decreases at higher altitudes.
Answer the following question.
State Newton’s law of gravitation and express it in vector form.
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
The _______ force is much weaker than other forces in nature.
Mahendra and Virat are sitting at a distance of 1 m from each other.Their masses are 75 kg and 80 kg respectively. What is the gravitational force between them? (G = 6.67 × 10-11 Nm2/kg2)
To project the rockets which of the following principle(s) is /(are) required?
State the universal law of gravitation and derive its mathematical expression.
Law of gravitation gives the gravitational force between
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube law- ______.
- planets will not have elliptic orbits.
- circular orbits of planets is not possible.
- projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.
- there will be no gravitational force inside a spherical shell of uniform density.
Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.
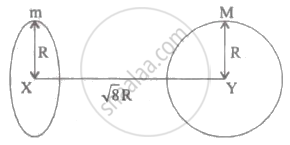
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
