Advertisements
Advertisements
प्रश्न
Choose the correct answer from among the given ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
Advertisements
उत्तर १
(ii)
Gravitational potential (V) is constant at all points in a spherical shell. Hence, the gravitational potential gradient (`"dV"/"dr"`)is zero everywhere inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. This indicates that gravitational forces acting at a point in a spherical shell are symmetric.
If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle at an arbitrary point P will be in the downward direction
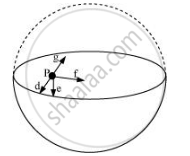
Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at an arbitrary point P of the hemispherical shell has the direction as indicated by arrow e.
उत्तर २
Using the explanation given in the solution of the previous problem, the direction of the gravitational field intensity at P will be along e. So, option (ii) is correct.
संबंधित प्रश्न
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
Explain the following:
People often shake the branches of a tree for getting down its fruits.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
How will the force of gravitation between two objects change if the distance between them is:
Halved
All objects in the universe attract each other along the line joining their________.
The force of attraction between any two material objects is called __________.
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the maximum height it would gain before it begins to fall.
A force can produce ________, In an object at rest. It can __________ an object and change its __________ of motion.
What does a force do in the following case?
You pull the skin of your arm
Name and state the action and reaction in the following case:
Hammering a nail.
What is the difference between gravity and gravitation?
Explain the difference between g and G.
Give the applications of universal law gravitation.
Law of gravitation gives the gravitational force between
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.
If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube law- ______.
- planets will not have elliptic orbits.
- circular orbits of planets is not possible.
- projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.
- there will be no gravitational force inside a spherical shell of uniform density.
Complete the chart below.
| F(N) | M1(kg) | M2(kg) | D(m) |
| (a) | 50 | 84 | 02 |
| 16 × 109 | 1.63 × 1022 | (b) | 34 |
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
