Advertisements
Advertisements
प्रश्न
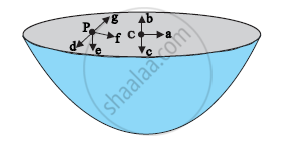
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
Advertisements
उत्तर १
At all points inside a hollow spherical shell, potential is same. So, gravitational intensity, which is negative of gravitational potential gradient, is zero. Due to zero gravitational intensity, the gravitational forces acting on any particle at any point inside a spherical shell will be symmetrically placed. It follows from here that if we remove the upper hemispherical shell, the net gravitational force acting on a particle at P will be downwards. Since gravitational intensity is gravitational force per unit mass therefore, the direction of gravitational intensity will be along c. So, option (iii) is correct.
उत्तर २
(iii)
Gravitational potential (V) is constant at all points in a spherical shell. Hence, the gravitational potential gradient (`"dV"/
"dr"`)
is zero everywhere inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. This indicates that gravitational forces acting at a point in a spherical shell are symmetric.
If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle located at centre O will be in the downward direction.
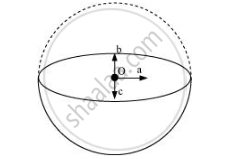
Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at centre O of the given hemispherical shell has the direction as indicated by arrow c.
संबंधित प्रश्न
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s −1 as it reaches A. The work done by the person on the mass is −3 J. The potential at A is
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the time it takes to reach this height.
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
What does a force do in the following case?
You apply brakes to a running car.
Name and state the action and reaction in the following case:
A book lying on a table.
Name and state the action and reaction in the following case:
A person walking on the ground.
Is there a gravitational attraction between you and the book? Explain.
The gravitational force between two bodies is directly proportional to the product of the masses of those bodies and is _______ of the distance between them.
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Shown are several curves (Figure). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.
If the mass of one object is doubled and distance remains the same, the gravitational force will:
The acceleration of the Moon towards the Earth is approximately:
