Advertisements
Advertisements
Question
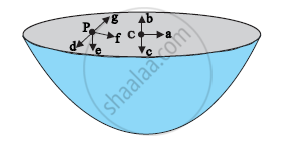
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
Advertisements
Solution 1
At all points inside a hollow spherical shell, potential is same. So, gravitational intensity, which is negative of gravitational potential gradient, is zero. Due to zero gravitational intensity, the gravitational forces acting on any particle at any point inside a spherical shell will be symmetrically placed. It follows from here that if we remove the upper hemispherical shell, the net gravitational force acting on a particle at P will be downwards. Since gravitational intensity is gravitational force per unit mass therefore, the direction of gravitational intensity will be along c. So, option (iii) is correct.
Solution 2
(iii)
Gravitational potential (V) is constant at all points in a spherical shell. Hence, the gravitational potential gradient (`"dV"/
"dr"`)
is zero everywhere inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. This indicates that gravitational forces acting at a point in a spherical shell are symmetric.
If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle located at centre O will be in the downward direction.
Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at centre O of the given hemispherical shell has the direction as indicated by arrow c.
APPEARS IN
RELATED QUESTIONS
What is the importance of the universal law of gravitation?
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
Explain the following:
People often shake the branches of a tree for getting down its fruits.
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
How will the force of gravitation between two objects change if the distance between them is:
Halved
Name and state the action and reaction in the following case:
Hammering a nail.
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
State Newton’s universal law of gravitation. Express it with the mathematical form of force of gravitation?
Give the applications of universal law gravitation.
For the weight of body of mass 5 kg to be zero on equator of the earth, angular velocity of the earth must be (The radius of earth = 6400 km, acceleration due to gravity = 10 m/s2).
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
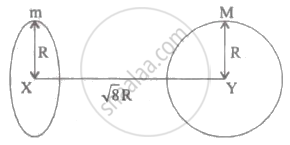
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.
Who measured the value of the Universal Gravitational Constant G using the Cavendish balance?
