Advertisements
Advertisements
प्रश्न
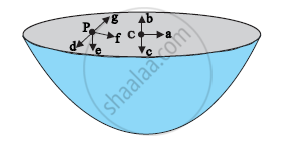
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
Advertisements
उत्तर १
At all points inside a hollow spherical shell, potential is same. So, gravitational intensity, which is negative of gravitational potential gradient, is zero. Due to zero gravitational intensity, the gravitational forces acting on any particle at any point inside a spherical shell will be symmetrically placed. It follows from here that if we remove the upper hemispherical shell, the net gravitational force acting on a particle at P will be downwards. Since gravitational intensity is gravitational force per unit mass therefore, the direction of gravitational intensity will be along c. So, option (iii) is correct.
उत्तर २
(iii)
Gravitational potential (V) is constant at all points in a spherical shell. Hence, the gravitational potential gradient (`"dV"/
"dr"`)
is zero everywhere inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. This indicates that gravitational forces acting at a point in a spherical shell are symmetric.
If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle located at centre O will be in the downward direction.
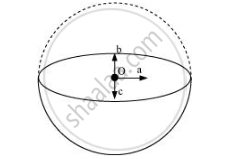
Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at centre O of the given hemispherical shell has the direction as indicated by arrow c.
APPEARS IN
संबंधित प्रश्न
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing altitude.
State Kepler’s law which is represented by the relation r3 ∝ T2.
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
Multiple Choice Question. Select the correct option.
The mass of earth is 6 × 1024 kg and radius of earth is 6.4 × 106 m. The magnitude of force between the mass of 1 kg and the earth is:
A ball is thrown up with a speed of 4.9 ms-1.
Prove that the time of ascent is equal to the time of descent.
A force can produce ________, In an object at rest. It can __________ an object and change its __________ of motion.
Explain why:
The atmosphere does not escape.
Explain the difference between g and G.
Is there a gravitational attraction between you and the book? Explain.
Give the applications of universal law gravitation.
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
Different points in earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m. For the earth-sun system (approximating the earth as a uniform density sphere).
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Observe the figure and answer the questions:
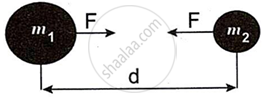
- State Newton's universal law of gravitation.
- If the distance between the two bodies is tripled, how will the gravitational force between them change?
- What will happen to gravitational force, if mass of one of the object is doubled?
