Advertisements
Advertisements
प्रश्न
Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
उत्तर

The orbit of a planet moving around the sun
Kepler’s first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
In the above figure, the elliptical orbit of a planet revolving around the sun. The position of the Sun is indicated by S.
Kepler’s second law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
A → B, C → D and E → F are the displacements of the planet in equal intervals of time.
The straight lines AS and CS sweep equal areas in equal intervals of time, i.e. area ASB and CSD are equal.
Kepler’s third law: The square of its period of revolution around the Sun is directly proportional to the cube of the mean distance of a planet from the Sun.
Thus, if r is the average distance of the planet from the Sun and T is its period of revolution then,
`"T"^2 α "r"^3 "i.e.," ("T"^2)/("r"^3) = "constant" = "K"`
For simplicity, we shall assume the orbit to be a circle.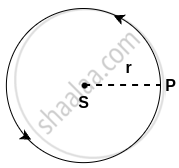
Circular motion of planet around the sun
S denotes the position of the Sun, P denotes the position of a planet at a given instant and r denotes the radius of the orbit (= the distance of the planet from the Sun). Here, the speed of the planet is uniform.
`"v" = "distance travelled"/"time taken"`
`= (2pir)/T`
If m is the mass of the planet, the centripetal force exerted on the planet by the Sun (= gravitational force),
`"F" = "mv"^2/r`
`"F" = (m((2pir)/"T")^2)/r`
`"F" = (4m pi^2r)/T^2`
Multiplying and dividing by r2 we get,
`"F" = (4 m pi^2)/r^2`
`"F" = (r^3/T^2)` ...(i)
According to Kepler’s third law,
`T^2/r^3 = K` ...(ii) [∵ K = constant]
Substituting (ii) in (i)
`"F" = (4m pi^2)/(K) xx 1/r^2`
F = `"constant" xx 1/r^2` [∵ where, `(4 m pi^2)/K = "constant"`]
∴ `F α 1/r^2`
APPEARS IN
संबंधित प्रश्न
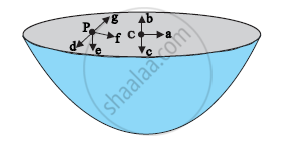
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
State the universal law of gravitation. Name the scientist who gave this law.
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s −1 as it reaches A. The work done by the person on the mass is −3 J. The potential at A is
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
Who stated the law of gravitation?
What does a force do in the following case?
You twist a piece of rubber.
Is there a gravitational attraction between you and the book? Explain.
Answer the following question.
State Newton’s law of gravitation and express it in vector form.
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
