Advertisements
Advertisements
Question
Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Solution

The orbit of a planet moving around the sun
Kepler’s first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
In the above figure, the elliptical orbit of a planet revolving around the sun. The position of the Sun is indicated by S.
Kepler’s second law: The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
A → B, C → D and E → F are the displacements of the planet in equal intervals of time.
The straight lines AS and CS sweep equal areas in equal intervals of time, i.e. area ASB and CSD are equal.
Kepler’s third law: The square of its period of revolution around the Sun is directly proportional to the cube of the mean distance of a planet from the Sun.
Thus, if r is the average distance of the planet from the Sun and T is its period of revolution then,
`"T"^2 α "r"^3 "i.e.," ("T"^2)/("r"^3) = "constant" = "K"`
For simplicity, we shall assume the orbit to be a circle.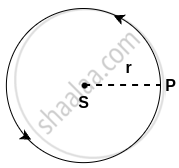
Circular motion of planet around the sun
S denotes the position of the Sun, P denotes the position of a planet at a given instant and r denotes the radius of the orbit (= the distance of the planet from the Sun). Here, the speed of the planet is uniform.
`"v" = "distance travelled"/"time taken"`
`= (2pir)/T`
If m is the mass of the planet, the centripetal force exerted on the planet by the Sun (= gravitational force),
`"F" = "mv"^2/r`
`"F" = (m((2pir)/"T")^2)/r`
`"F" = (4m pi^2r)/T^2`
Multiplying and dividing by r2 we get,
`"F" = (4 m pi^2)/r^2`
`"F" = (r^3/T^2)` ...(i)
According to Kepler’s third law,
`T^2/r^3 = K` ...(ii) [∵ K = constant]
Substituting (ii) in (i)
`"F" = (4m pi^2)/(K) xx 1/r^2`
F = `"constant" xx 1/r^2` [∵ where, `(4 m pi^2)/K = "constant"`]
∴ `F α 1/r^2`
APPEARS IN
RELATED QUESTIONS
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Answer the following:
An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
The law of gravitation gives the gravitational force between :
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
Define one Newton. How much maximum acceleration can it produce in a mass of 1 kg?
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
What is meant by the equation :
`g= Gxxm/r^2`
where the symbols have their usual meanings.
What does a force do in the following case?
You twist a piece of rubber.
You can change the direction in which an object is moving by___________.
Why does a ball moving on a table top eventually stops?
Gravity is another kind of ________. It exerts all through the ________. The Sun's gravity keeps the ___________ in their orbits. Gravity can only be felt with very large ________.
Is there a gravitational attraction between you and the book? Explain.
State Newton's universal law of gravitation. Express it with the mathematical form of force of gravitation?
State the universal law of gravitation and derive its mathematical expression.
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Newton's universal law of gravitation applies to ______.
