Advertisements
Advertisements
Question
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
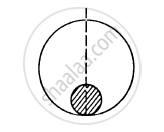
Solution
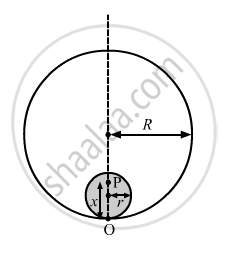
(a) Consider that the particle is placed at a distance x from O.
Here, r < x < 2r
Let us consider a thin solid sphere of radius (x \[-\] r).
Mass of the sphere,
\[dm = \frac{m}{\left( \frac{4}{3} \right)\pi r^3} \times \frac{4}{3}\pi(x - r )^3 = \frac{m(x - r )^3}{r^3}\]
Then the gravitational force on the particle due to the solid sphere is given by
\[F = \frac{Gm' dm}{(x - r )^2}\]
\[ = \frac{G\frac{m(x - r )^3}{r^3}m'}{(x - r )^2} = \frac{Gmm'(x - r)}{r^3}\]
Force on the particle due to the shell will be zero because gravitational field intensity inside a shell is zero.
(b) If 2r < x < 2R,
Force on the body due to the shell will again be zero as particle is still inside the shell.
then F is only due to the solid sphere.
\[\therefore F = \frac{Gmm'}{\left( x - r \right)^2}\]
(c) If x > 2R, then the gravitational force is due to both the sphere and the shell.
Now, we have :
Gravitational force due to shell,
\[F = \frac{GMm'}{\left( x - R \right)^2}\]
Gravitational force due to the sphere \[= \frac{Gmm'}{\left( x - r \right)^2}\]
As both the forces are acting along the same line joining the particle with the centre of the sphere and shell so both the forces can be added directly without worrying about their vector nature.
∴ Resultant force \[= \frac{Gmm'}{\left( x - r \right)^2} + \frac{GMm'}{\left( x - R \right)^2}\]
APPEARS IN
RELATED QUESTIONS
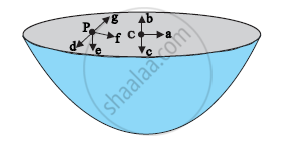
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
State two applications of universal law of gravitation.
Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements :
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
The mass of moon is about 0.012 times that of earth and its diameter is about 0.25 times that of earth. The value of G on the moon will be:
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
Where will you weigh more: at the centre of the earth or at the surface of the earth?
Show that gravity decreases at higher altitudes.
As observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from earth, this would ______.
Give scientific reasons for the following:
Newton's gravitational law is the universal law of gravitation.
Complete the chart below.
| F(N) | M1(kg) | M2(kg) | D(m) |
| (a) | 50 | 84 | 02 |
| 16 × 109 | 1.63 × 1022 | (b) | 34 |
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.
Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.
