Advertisements
Advertisements
Question
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Solution
Three spheres are placed with their centres at A, B and C as shown in the figure.
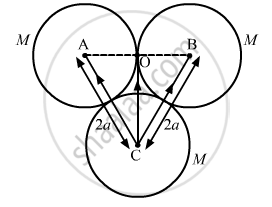
Gravitational force on sphere C due to sphere B is given by
\[\overrightarrow {F}_{CB} = \frac{G m^2}{4 a^2}\cos 60^\circ \hat i + \frac{G m^2}{4 a^2} \cdot \sin 60^\circ \hat j\]
Gravitational force on sphere C due to sphere A is given by \[\overrightarrow {F}_{CA} = - \frac{G m^2}{4 a^2} \cos 60^\circ\hat i + \frac{G m^2}{4 a^2} \cdot \sin 60^\circ\hat j\]
\[\therefore {\overrightarrow F}_{CB} = \overrightarrow {F}_{CB} + \overrightarrow {F}_{CA} \]
\[ = + \frac{2G m^2}{4 a^2}\sin 60^\circ \hat j \]
\[ = + \frac{2G m^2}{4 a^2} \times \frac{\sqrt{3}}{2}\]
i.e., magnitude \[= \frac{\sqrt{3} G m^2}{4 a^2}\] along CO
APPEARS IN
RELATED QUESTIONS
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
What is the importance of the universal law of gravitation?
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
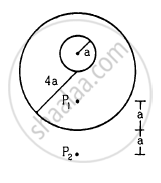
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
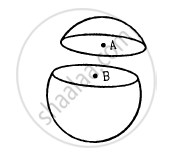
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
How will the force of gravitation between two objects change if the distance between them is:
Infinite
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
The force of attraction between any two material objects is called __________.
Where will you weigh more: at the centre of the earth or at the surface of the earth?
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
Name and state the action and reaction in the following case:
Hammering a nail.
Why does a ball moving on a table top eventually stops?
An apple falls towards the earth due to its gravitational force. The apple also attracts the earth with the same force. Why do we not see the earth rising towards the apple? Explain.
Show that gravity decreases at higher altitudes.
The gravitational force between two bodies is directly proportional to the product of the masses of those bodies and is _______ of the distance between them.
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.
