Advertisements
Advertisements
Question
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Solution
Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = \[\sqrt{2}a\]
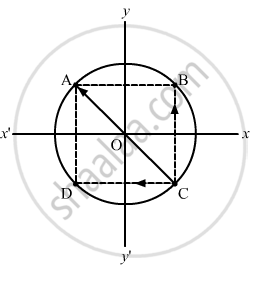
The force on the particle at C due to gravitational attraction of the particle at B is
\[\overrightarrow{F}_{CB} = \frac{G M^2}{2 R^2} \hat j\] .
The force on the particle at C due to gravitational attraction of the particle at D is
\[\overrightarrow{F}_{CD} = - \frac{G M^2}{2 R^2} \hat i\].
Now, force on the particle at C due to gravitational attraction of the particle at A is given by
\[\overrightarrow{F}_{CA} = - \frac{G M^2}{4 R^2}\cos 45 \hat i + \frac{G M^2}{4 R^2}\sin 45 \hat j\]
\[ \therefore \overrightarrow{F}_C = \overrightarrow{F}_{CA} + \overrightarrow{F}_{CB} + \overrightarrow{F}_{CD} \]
\[ = \frac{- G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat i + \frac{G M^2}{4 R^2}\left( 2 + \frac{1}{\sqrt{2}} \right) \hat j\]
So, the resultant gravitational force on C is \[F_C = \frac{G m^2}{4 R^2}\sqrt{2\sqrt{2} + 1}\]
Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by
\[F = \frac{m v^2}{R}\]
\[ \Rightarrow v = \sqrt{\frac{GM}{R}\left( \frac{2\sqrt{2} + 1}{4} \right)}\]
APPEARS IN
RELATED QUESTIONS
If the moon attracts the earth, why does the earth not move towards the moon?
What is the importance of the universal law of gravitation?
State two applications of universal law of gravitation.
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
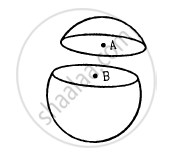
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
Multiple Choice Question. Select the correct option.
The mass of earth is 6 × 1024 kg and radius of earth is 6.4 × 106 m. The magnitude of force between the mass of 1 kg and the earth is:
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the time it takes to reach this height.
Where will you weigh more: at the moon's surface or at the earth's surface?
What does a force do in the following case?
You apply brakes to a running car.
Name and state the action and reaction in the following case:
A book lying on a table.
Two equal and opposite forces acting at the same point on a stationary body. Will the body move? Give reason to explain your answer.
What is the difference between gravity and gravitation?
Does the force of the earth's gravitation affect the motion of the moon? Explain your answer with reasons.
The distance-time values for an object moving along straight line are given below:
| Time (s) | Distance (m) |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
State the universal law of gravitation and derive its mathematical expression.
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
