Advertisements
Advertisements
Question
State the universal law of gravitation and derive its mathematical expression.
Solution
This law states that every particle of matter in this universe attracts every other particle with a force. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centers of these masses. The direction of the force acts along the line joining the masses.
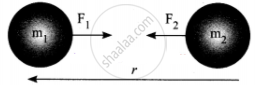
gravitational force between two masses
The force between the masses is always attractive and it does not depend on the medium where they are placed.
Let, m1 and m2 be the masses of two bodies A and B placed r metre apart in space.
Force F ∝ m1 × m2
F ∝ 1/r2
On combining the above two expressions
F ∝ `("m"_1xx"m"_2)/"r"^2`
F = `("Gm"_1"m"_2)/r^2`
Where G is the universal gravitational constant.
Its value in SI unit is 6.674 × 10-11 Nm2 kg-2.
APPEARS IN
RELATED QUESTIONS
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing depth. (assume the earth to be a sphere of uniform density).
Can you think of two particles which do not exert gravitational force on each other?
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
How will the force of gravitation between two objects change if the distance between them is:
Infinite
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the maximum height it would gain before it begins to fall.
Name and state the action and reaction in the following case:
Hammering a nail.
