Question

Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.

Answer 1

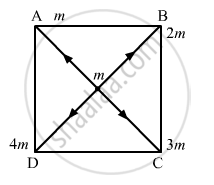
\[\text { Force due to the particle at A }, \overrightarrow{F}_{OA} = \frac{G \times m \times m}{{OA}^2}\]

\[\text { Let OA } = r\]

\[ \therefore \overrightarrow{F}_{OA} = \frac{G \times m \times m}{r^2} \]

\[\text { Here }, r = \sqrt{\left( \frac{a}{2} \right)^2 + \left( \frac{a}{2} \right)^2} = \frac{a}{\sqrt{2}}\]

\[\text { Force due to the particle at B }, \overrightarrow{F}_{OB} = \frac{G \times m \times 2m}{r^2}\]

\[\text { Force due to the particle at C }, \overrightarrow{F}_{OC} = \frac{G \times m \times 3m}{r^2}\]

\[\text { Force due to the particle at D }, \overrightarrow{F}_{OD} = \frac{G \times m \times 4m}{r^2}\]

\[\text { Now, resultant force }= \overrightarrow{F}_{OA} + \overrightarrow{F}_{OB} + \overrightarrow{F}_{OC} + \overrightarrow{F}_{OD} \]

\[ = \frac{2Gmm}{a^2}\left[ - \frac{\overrightarrow{i}}{\sqrt{2}} + \frac{\overrightarrow{j}}{\sqrt{2}} \right] + \frac{4Gmm}{a^2}\left[ \frac{\overrightarrow{i}}{\sqrt{2}} + \frac{\overrightarrow{j}}{\sqrt{2}} \right]\]

\[ = \frac{6Gmm}{a^2}\left[ \frac{\overrightarrow{i}}{\sqrt{2}} - \frac{\vec{j}}{\sqrt{2}} \right] + \frac{8Gmm}{a^2}\left[ \frac{- \overrightarrow{i}}{\sqrt{2}} - \frac{- \overrightarrow{j}}{\sqrt{2}} \right]\]

\[ \therefore F = \frac{4\sqrt{4}G m^2}{a^2} \stackrel\frown {j}\]