Advertisements
Advertisements
Question
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Solution
Given: MS = 1.99 × 1030 kg, ME = 5.98 × 1024 kg, R = 1.5 × 1011 m
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = `("Gm"_1"m"_2)/"r"^2`
Calculation: As, we know, G = 6.67 × 10–11 N m2/kg2
From formula,
F = `("GM"_"s""M"_"E")/"R"^2`
`= (6.67 xx 10^-11 xx 1.99 xx 10^30 xx 5.98 xx 10^24)/(1.5 xx 10^11)^2`
∴ F = `(6.67 xx 1.99 xx 5.98)/2.25 xx 10^21`
= antilog{(log(6.67) + log(1.99) + log(5.98) - log(2.25)} × 1021
= antilog{(0.8241) + (0.2989) + (0.7767) - (0.3522)} × 1021
= antilog{1.5475} × 1021
= 35.28 × 1021
= 3.5 × 1022 N
The gravitational force between the Sun and the Earth is = 3.5 × 1022 N.
APPEARS IN
RELATED QUESTIONS
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
A person sitting in a chair in a satellite feels weightless because
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Explain the following:
People often shake the branches of a tree for getting down its fruits.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
How will the force of gravitation between two objects change if the distance between them is:
Doubled
A ball is thrown up with a speed of 4.9 ms-1.
Prove that the time of ascent is equal to the time of descent.
Where will you weigh more: at the moon's surface or at the earth's surface?
What does a force do in the following case?
You apply brakes to a running car.
What does a force do in the following case?
You catch a kicked ball.
Name and state the action and reaction in the following case:
A book lying on a table.
Name and state the action and reaction in the following case:
A person walking on the ground.
What is the difference between gravity and gravitation?
Answer the following question.
State Newton’s law of gravitation and express it in vector form.
The _______ force is much weaker than other forces in nature.
The force of gravitation between two bodies of mass 1 kg each separated by a distance of 1 m in vacuum is ____________.
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
Give scientific reasons for the following:
Newton's gravitational law is the universal law of gravitation.
Complete the chart below.
| F(N) | M1(kg) | M2(kg) | D(m) |
| (a) | 50 | 84 | 02 |
| 16 × 109 | 1.63 × 1022 | (b) | 34 |
Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.
Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.
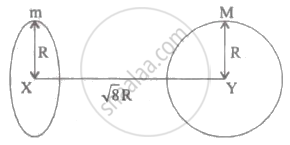
Observe the figure and answer the questions:
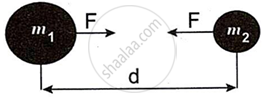
- State Newton's universal law of gravitation.
- If the distance between the two bodies is tripled, how will the gravitational force between them change?
- What will happen to gravitational force, if mass of one of the object is doubled?
