Advertisements
Advertisements
Question
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Solution
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
When a planet is moving in an elliptical orbit, at some point, the line joining the centre of the Sun and the planet is perpendicular to the velocity of the planet. For that instant, work done by the gravitational force on the planet becomes zero. As there is no net increase in the speed of the planet after one complete revolution about the Sun, the work done by the gravitational force on the planet in one complete revolution is zero.
Note:For elliptical orbits angle between force ans velocity is always 90 so there the work done is zero in any small part of the orbit.
APPEARS IN
RELATED QUESTIONS
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
What happens to the force between two objects, if the masses of both objects are doubled?
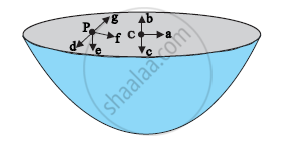
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Can you think of two particles which do not exert gravitational force on each other?
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s −1 as it reaches A. The work done by the person on the mass is −3 J. The potential at A is
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
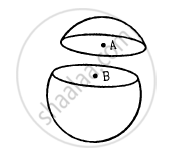
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
How will the force of gravitation between two objects change if the distance between them is:
Halved
The force of attraction between any two material objects is called __________.
Is the law of gravitation applicable in case of the sun and the moon?
Where will you weigh more: at the moon's surface or at the earth's surface?
Explain the difference between g and G.
State Newton's law of gravitation. What is the difference between:
Gravity and gravitation
To project the rockets which of the following principle(s) is /(are) required?
Answer the following questions in reference to the figure below:
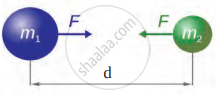
- Which relation is shown in the figure?
- What will happen if the mass of one of the objects is doubled?
Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.
