Advertisements
Advertisements
Question
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Solution
A particle will be in equilibrium when the net force acting on it is equal to zero. Two particles under the action of their mutual gravitational force will be in equilibrium when they revolve around a common point under the influence of their mutual gravitational force of attraction. In this case, the gravitational pull is used up in providing the necessary centripetal force. Hence, the net force on the particles is zero and they are in equilibrium. This is also true for a three particle system.
APPEARS IN
RELATED QUESTIONS
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
If the moon attracts the earth, why does the earth not move towards the moon?
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
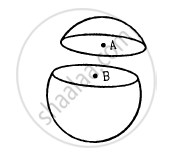
Explain the following:
People often shake the branches of a tree for getting down its fruits.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
What does a force do in the following case?
You catch a kicked ball.
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
State the universal law of gravitation and derive its mathematical expression.
Law of gravitation gives the gravitational force between
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

Shown are several curves (Figure). Explain with reason, which ones amongst them can be possible trajectories traced by a projectile (neglect air friction).
Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.
Observe the figure and answer the questions:
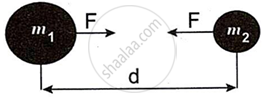
- State Newton's universal law of gravitation.
- If the distance between the two bodies is tripled, how will the gravitational force between them change?
- What will happen to gravitational force, if mass of one of the object is doubled?
